State Space Duality (Mamba-2) Part III - The Algorithm
- Part I - The Model
- Part II - The Theory
- Part III - The Algorithm
- Part IV - The Systems
The theoretical framework of structured state space duality (see Part I and Part II of this series) connects SSMs and (linear) attention through structured matrices. As mentioned in Part I, this connection allows us to derive new algorithms for selective SSMs that are faster than the parallel associative scan in Mamba-1 by leveraging matrix multiplication as a primitive. Moreover, the connection can bring system optimizations (e.g. tensor parallelism, sequence parallelism, variable sequence length) originally developed for Transformer to SSM-land.
The SSD Algorithm
Even though we already developed optimized scans implementations for Mamba-1, we were limited to small state expansion (typically $\mathtt{N}=16$) as the algorithm and implementation did not use tensor cores (specialized hardware units that perform matrix multiplication). Typically matrix multiplication (matmul) FLOPs are much faster (up to 16x) than non-matmul FLOPs: the A100 GPU has 312 TFLOPS of BF16 matmul but only 19 TFLOPS of FP32 arithmetics, and the H100 has 989 TFLOPS of BF16 matmul but only 67 TFLOPS of FP32 arithmetics. One of our primary goals with Mamba-2 is to leverage tensor cores to speed up the SSM.
To recap, after tying parameters and introducing the head structure, the SSM in Mamba-1 turns into SSD, a more restrictive form that has an attention-like formulation. And as SSD connects SSMs and structured matrices, we saw in Part II that efficient algorithms to compute SSMs correspond directly to different decompositions of the “token-mixing” or “sequence-mixing” matrix $M$.
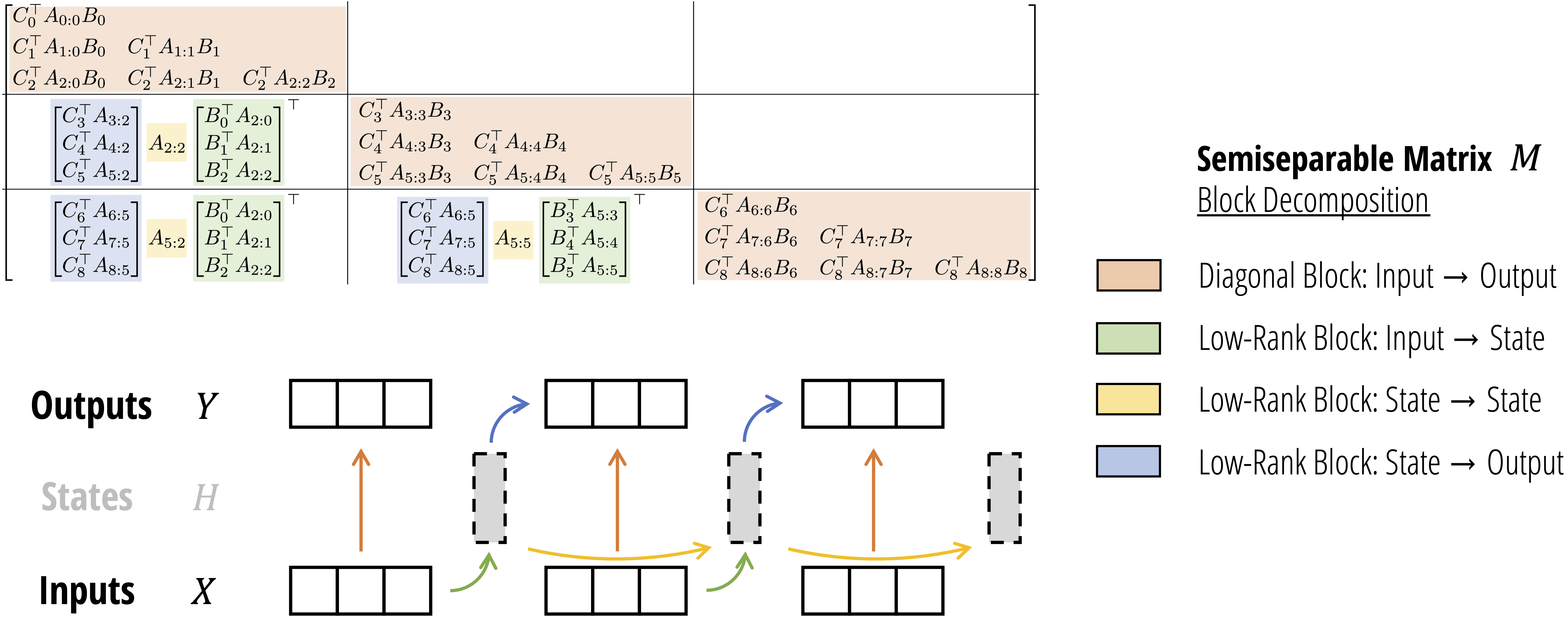
We can therefore create new algorithms to compute SSMs simply by looking for alternative ways to multiply this matrix, for example by decomposing it in various ways. A simple block decomposition of this matrix, with carefully chosen block sizes, turns out to get all the advantages of both the linear-recurrent and quadratic-attention dual forms of SSD. This leads to the SSD algorithm, which has 4 steps. There are two completely different interpretations of this algorithm!
SSD Algorithm: Block Matrix Decomposition
We first partition the SSM (semiseparable) matrix into blocks of size $\mathtt{Q} \times \mathtt{Q}$. Then, we use the properties of semiseparable matrices to factorize each off-diagonal block, which is low rank.
- (Orange) Each diagonal block is a smaller semiseparable matrix; we can compute this multiplication however we like; in particular, using the quadratic (attention-like) form of SSD.
- (Green) There are only $\mathtt{T} / \mathtt{Q}$ total different green blocks because many of them are shared. These can be computed with a batched matmul.
- (Yellow) Notice that the yellow terms themselves form a 1-semiseparable matrix; in other words, this step is equivalently to an SSM scan (on some modified $A$ factors)!
- (Blue) Similar to green, these can be computed with a batched matmul.
SSD Algorithm: Chunking and State Passing
An alternative interpretation of the algorithm involves reasoning about how the SSM operates on the actual sequence. We first split the sequence of input into blocks (or chunks) of size $\mathtt{Q}$. The steps then have the interpretation
- Intra-chunk outputs: compute the local output of each chunk (what is the output per chunk supposing that the initial state (to the chunk) is 0?)
- Chunk states: compute the final state of each chunk (what is the final state per chunk supposing that the initial state (to the chunk) is 0?)
- Pass states: compute a recurrence on all of the chunks’ final states – using any desired algorithm, e.g. parallel or sequential scan (what is the actual final state per chunk taking into account all previous inputs?)
- Output states: for each chunk, given its true initial state (computed in Step 3), compute the contribution to the output just from the initial state
Either way, we see that most of the algorithm (Step 1, 2, and 4) leverages matmuls (and hence tensor cores), and also can be computed completely in parallel! Only Step 3 requires a scan, but it operates on a much shorter sequence and usually only takes a small fraction of the time of the full algorithm.
Special Cases
We note that special cases of this algorithm have been seen before. In particular RetNet
Other forms of “chunkwise” recurrences have recently become popular, such as in Gated Linear Attention (GLA)
The Code
In the “Minimal SSD” code that we provide in the paper and the code release, we delineate each of these four steps. As promised, this algorithm is not only faster but also much easier to implement than the original selective scan of Mamba, coming in at just around 25 lines of code!
def segsum(x):
"""Naive segment sum calculation. exp(segsum(A)) produces a 1-SS matrix,
which is equivalent to a scalar SSM."""
T = x.size(-1)
x_cumsum = torch.cumsum(x, dim=-1)
x_segsum = x_cumsum[..., :, None] - x_cumsum[..., None, :]
mask = torch.tril(torch.ones(T, T, device=x.device, dtype=bool), diagonal=0)
x_segsum = x_segsum.masked_fill(~mask, -torch.inf)
return x_segsum
def ssd(X, A, B, C, block_len=64, initial_states=None):
"""
Arguments:
X: (batch, length, n_heads, d_head)
A: (batch, length, n_heads)
B: (batch, length, n_heads, d_state)
C: (batch, length, n_heads, d_state)
Return:
Y: (batch, length, n_heads, d_head)
"""
assert X.dtype == A.dtype == B.dtype == C.dtype
assert X.shape[1] % block_len == 0
# Rearrange into blocks/chunks
X, A, B, C = [rearrange(x, "b (c l) ... -> b c l ...", l=block_len) for x in (X, A, B, C)]
A = rearrange(A, "b c l h -> b h c l")
A_cumsum = torch.cumsum(A, dim=-1)
# 1. Compute the output for each intra-chunk (diagonal blocks)
L = torch.exp(segsum(A))
Y_diag = torch.einsum("bclhn,bcshn,bhcls,bcshp->bclhp", C, B, L, X)
# 2. Compute the state for each intra-chunk
# (right term of low-rank factorization of off-diagonal blocks; B terms)
decay_states = torch.exp((A_cumsum[:, :, :, -1:] - A_cumsum))
states = torch.einsum("bclhn,bhcl,bclhp->bchpn", B, decay_states, X)
# 3. Compute the inter-chunk SSM recurrence; produces correct SSM states at chunk boundaries
# (middle term of factorization of off-diag blocks; A terms)
if initial_states is None:
initial_states = torch.zeros_like(states[:, :1])
states = torch.cat([initial_states, states], dim=1)
decay_chunk = torch.exp(segsum(F.pad(A_cumsum[:, :, :, -1], (1, 0))))
new_states = torch.einsum("bhzc,bchpn->bzhpn", decay_chunk, states)
states, final_state = new_states[:, :-1], new_states[:, -1]
# 4. Compute state -> output conversion per chunk
# (left term of low-rank factorization of off-diagonal blocks; C terms)
state_decay_out = torch.exp(A_cumsum)
Y_off = torch.einsum('bclhn,bchpn,bhcl->bclhp', C, states, state_decay_out)
# Add output of intra-chunk and inter-chunk terms (diagonal and off-diagonal blocks)
Y = rearrange(Y_diag+Y_off, "b c l h p -> b (c l) h p")
return Y, final_state
The Details
Let’s talk about a couple of additional details in the implementation (these don’t even appear in the full paper, so pay attention!) that unpack some of the choices in this reference code.
The SSM Scan
In the above code, we utilized the connection between scalar SSM recurrences
\[h_{t+1} = A_t h_t + B_t x_t\]and matrix multiplication by 1-semiseparable matrices
\[L = \begin{bmatrix} 1 & \\ a_1 & 1 & \\ a_2a_1 & a_2 & 1 \\ \vdots & \vdots & \ddots & \ddots \\ a_{\mathtt{T}-1}\dots a_1 & a_{\mathtt{T}-1}\dots a_2 & \dots & a_{\mathtt{T}-1} & 1 \\ \end{bmatrix}\]which we covered in Part II (and Section 3.2.2 of the paper). In this minimal implementation, we compute Step 3 of the algorithm, which is computing a scalar SSM by any algorithm of our choice, by explicitly materializing a 1-SS matrix and doing dense matrix multiplication.
We use this version for several reasons:
- Code-wise, it’s simpler to materialize and multiply by this matrix than to actually implement a parallel associative scan
- Because of the block decomposition of the SSM matrix, the sequence length $\mathtt{T}$ is reduced by a factor of $\approx 100$ – so doing the scan in time $O(\mathtt{T}^2)$ instead of $O(\mathtt{T})$ isn’t too bad
- We have to materialize a 1-SS matrix anyways for Step 1 of the algorithm (the diagonal blocks), so might as well reuse the code ¯\_(ツ)_/¯
While this example code is simpler and reasonably efficient on GPU (and probably TPU as well!), it’s no longer truly linear at long sequences. Our more optimized Triton implementation does replace the 1-SS multiplication in Step 3 with an actual associative scan.
Stability
Attempt 1: Ratios of cumprods
The first naive attempt may be to notice that the entries of this matrix are cumulative products
\[a_{i:j}^\times = a_i \times \cdots \times a_{j-1} = \frac{a_{i:\mathtt{T}}^\times}{a_{j:\mathtt{T}}^\times}\]However, this runs into severe numerical issues because these products can get really tiny (imagine $a_t \approx 0.9$ and powering it up for a sequence length $\mathtt{T}$ in the thousands!)
Fix 1: The Segment Sum (segsum) Operation
The second attempt would be to do all of this in log-space, because all the $a_t$ are positive; so the products become additions, and instead of cumprods to deal with we have cumsums instead. Then in order to compute the 1-SS matrix, we just have to compute the sums $\log a_i + \dots + \log a_{j-1}$ for every segment $[i:j]$. We call this the segment sum (segsum) primitive, analogous to cumulative sum (cumsum).
Attempt 2: Differences of cumsums
The obvious way to do this again is using the same idea as above, but in log space
\[a_{i:j}^\times = \exp\left( \log a_i + \cdots + \log a_{j-1} \right) = \left( (\log a)_{i:\mathtt{T}}^+ - (\log a)_{j:\mathtt{T}}^+ \right)\]where we compute a single cumulative sum of $a$ along the time axis, and then compute all pairwise differences. In code, we can do this with
def segsum_unstable(x):
"""Naive segment sum calculation."""
T = x.size(-1)
x_cumsum = torch.cumsum(x, dim=-1)
x_segsum = x_cumsum[..., :, None] - x_cumsum[..., None, :]
mask = torch.tril(torch.ones(T, T, device=x.device, dtype=bool), diagonal=0)
x_segsum = x_segsum.masked_fill(~mask, -torch.inf)
return x_segsum
(and then the 1-semiseparable matrix is just the exponential of this output).
Sums/differences are a lot more stable than products/quotients, so this should work – right?
Fix 2: Remove All Subtractions
Unfortunately, it turns out this still doesn’t work. The values of this 1-SS matrix roughly represent the SSM dynamics, which are very sensitive to these values of $a_t$, so we have to be very precise. And even in log space, these cumsums can be fairly large, which runs into catastrophic cancellation when subtracted. So we really have to find a way to compute this matrix with only additions, while still vectorizing everything…
Attempt 3: Stable Segsum
This leads to the helper function in the reference SSD code. Instead of computing a single cumsum and then subtracting, we find a way to use a batch of independent cumsums that immediately produces the right answer without subtraction.
These details do matter! Without the right implementation of these primitives, the basic SSD algorithm produces NaNs immediately during training (even with FP32).
Discretization
This lineage of structured state space models developed from S4 and its predecessors which were viewed as continuous-time systems.
In Mamba, however, we don’t really view the SSM as continuous anymore. In fact, as mentioned in the Discussion (Section 5) of the original paper, Mamba trades off with S4 on modeling different types of data:
- S4 is a continuous-time model that excels at modeling continuous data, e.g. perceptual signals such as audio waveforms and pixel-level vision.
- Mamba is a discrete-time model that excels at modeling discrete data, e.g. tokenized data such as language.
However, the parameterization of Mamba still used the same discretization step as in prior structured SSMs, where there is another parameter $\Delta$ being modeled. We do this because the discretization step has other side effects such as properly normalizing the activations
The initializations and parameterizations from the previous theory on structured SSMs still work out-of-the-box, so why fix what’s not broken?
Despite this, we’re pretty sure that the discretization step isn’t really necessary for Mamba. In the Mamba-2 paper, we chose to work directly with the “discrete parameters” $A$ and $B$, which in all previous structured SSM papers (including Mamba-1) were denoted $(\bar{A}, \bar{B})$ and defined through an additional transformation
\[\begin{align*} \bar{A} &= \exp(e^{\Delta A}) \\ \bar{B} &= (\exp(e^{\Delta A}) - I) A^{-1} B \end{align*}\]This doesn’t pose any problems: to use the continuous SSM parameterization, simply transform the parameters through the above formulas before plugging into the SSD code above.
In the full Mamba-2 code, we also kept the same parameterization and discretization step as in Mamba—again, why fix what’s not broken?—but hypothesize that “discrete-centric” variants (such as the gamma normalization of LRU
Is Discretization Necessary?
It’s useful for other structured SSMs, but perhaps not needed for Mamba. But it’s just a simple invertible transformation, so use either discrete or continuous parameterizations as you like!
What’s Next
In the final part of this series, we’ll continue talking about the implementation of Mamba-2, but on a more macroscopic level; about the entire neural network, instead of just details of the core SSD layer.
We’ll also talk about the actual speed of the algorithm covered in this post.