Muon is becoming the optimizer of choice for training state-of-the-art language models like Kimi K2 Thinking and GLM-5.¹² Compared to AdamW, Muon needs fewer optimizer steps to reach a given loss, but each step is more expensive. This overhead is due to Muon’s Newton-Schulz orthogonalization procedure, a cubic time matrix operation not present in older optimizers.

Figure 1: AdamW vs. Muon: Wall clock time of optimizer step across LLaMa model sizes, benchmarked on B300.

Muon’s superior optimization quality justifies its more expensive optimizer step. However, as model size scales up, the overhead of computing each Muon step grows rapidly. Traditional optimization methods (SGD, AdamW) perform element-wise operations, such as updating the momentum or rescaling it by the second moment. For a weight matrix of size $n \times m$, performing the optimizer step takes $O(mn)$ time given the gradient matrix as input. In contrast, many modern optimizers (Muon, Scion, Dion, SOAP, Shampoo, SPlus, etc.) use orthogonalization or higher-order preconditioning to compute the update to the weights at each training step.³⁴⁵⁶⁷⁸ These methods require matrix multiplications that cost $O(mn^2)$ time (assuming $n \leq m$). Therefore, the runtime of each call to the optimizer is far greater than for AdamW. Depending on the training setup (global batch size, cluster size, and parallelism settings), Newton-Schulz accounts for between 2% and 17% of end-to-end wall clock time.

While $O(mn^2)$ runtime is an unavoidable cost of these algorithms, there is still significant room for improvement in both FLOPs and wall clock time. As it is typically implemented, the Newton-Schulz routine has several shortcomings:

1. It uses not just one or two, but ten multiplications of $n \times m$ matrices, costing $2mn^2$ FLOPs each. Most weights in popular architectures are rectangular, with $m \gg n$, and those of recent MoE architectures with many fine-grained experts are even more rectangular. Thus, the rectangular matrix multiplications dominate the costs of other operations (like small multiplications of $n \times n$ matrices).
2. Many of the intermediate matrices it computes are symmetric, but no computational advantage is taken of this structure. Half the work used to compute these matrices is redundant.
3. It uses cuBLAS for batched matrix multiplication/addition $\alpha \mathbf A \mathbf B + \beta \mathbf C$, which is not fully optimized for the Hopper GPU architecture.

Previous work has sought to improve Newton-Schulz by optimizing its polynomial coefficients or its normalization step. While this can reduce the number of iterations needed for Newton-Schulz to converge, it does not address the shortcomings listed above. Others⁹ have implemented Newton-Schulz using special-purpose symmetric matrix multiplication routines, but the runtime benefit is limited due to the high number of rectangular and non-symmetric multiplications. While Newton-Schulz and related methods have been studied for decades in the numerical analysis literature, research attention has mostly focused on regimes where high accuracy is required, where algorithms are optimized for CPUs rather than GPUs, or where input matrices are square. In recent years, randomized sketching has been used to design sophisticated algorithms for many computations involving highly rectangular matrices; however (aside from further optimizing the coefficients¹⁰) these do not seem to be applicable to Muon.

Our Contributions

To address these shortcomings, we introduce Gram Newton-Schulz, a reworking of the Newton-Schulz routine that reduces the optimizer time by up to 50% in trillion-parameter MoE models like Kimi K2. Instead of iterating on the rectangular input matrix $\mathbf{X} \in \mathbb{R}^{n \times m}$, Gram Newton-Schulz iterates on the small square symmetric Gram matrix $\mathbf{XX^\top} \in\mathbb{R}^{n \times n}$, reducing the FLOP cost and enabling a greater use of symmetric GEMM kernels.

Our contributions are as follows. First, we show how to rewrite standard Newton-Schulz in a form that is mathematically identical, producing the exact same output up to floating-point error, but that acts mostly on the space of $n \times n$ matrices. Because these matrices are smaller and admit specialized symmetric matrix multiplication routines, each iteration is faster than in standard Newton-Schulz. Only the preprocessing step (forming $\mathbf X \mathbf X^\top$) and the post-processing step (multiplying by $\mathbf X$) require rectangular matrix multiplications. We call this new form Naive Gram Newton-Schulz.

Second, we conduct a thorough study of the numerical properties of Naive Gram Newton-Schulz. We identify the potential for numerical instability when using half-precision floating point arithmetic, especially due to spurious negative eigenvalues in the Gram matrix. We remedy this instability using a “restarting” strategy, where we reconstruct the Gram matrix partway through the algorithm. We call this modified algorithm Stabilized Gram Newton-Schulz.

Third, to take full advantage of the latest generation of GPUs and of the mathematical structure of Newton-Schulz, we implement custom kernels for symmetric matrix multiplication. The kernels, implemented in CuTeDSL for the Hopper and Blackwell architectures, attain state-of-art performance.

Finally, we replace Muon’s Newton-Schulz routine with Gram Newton-Schulz, an optimizer we call GramMuon, and observe a 40-50% reduction in the runtime of the orthogonalization step. Experiments confirm that training language models with GramMuon is stable and preserves the optimization quality of the standard version within $0.01$ validation perplexity, making our algorithm a rare instance of “free lunch” performance improvement.

To facilitate the adoption of Gram Newton-Schulz, we release the following open-source implementations:

1. A drop-in replacement for Muon’s Newton-Schulz routine that is mathematically equivalent, numerically stable, and up to twice as fast.
2. Fast GPU kernels for symmetric matrix multiplication ($AB$, $\alpha AB + \beta C$) written in CuTeDSL for Hopper and Blackwell, which may be of independent interest.

We will begin by recapping Muon to see why we need Newton-Schulz in the first place, describing how standard Newton-Schulz works mathematically, and analyzing its performance bottlenecks.

Muon Recap

The Muon optimizer³ is best described as steepest-direction descent with respect to the spectral norm.¹¹ At step $k$ of training, let $\mathbf W_k \in \mathbb{R}^{n \times m}$ be a weight matrix and let $\mathbf G_k$ be the gradient of the loss with respect to $\mathbf W_k$. The Muon update rule is

where $\mu$ is the momentum coefficient, $\eta$ is the learning rate, and $\mathbf M_k$ is the momentum matrix (with $\mathbf M_0 := 0$).

In most ways, Muon resembles basic stochastic gradient descent (SGD) with momentum. Its key innovation is using the $\operatorname{polar}$ operation, which is defined as follows:

Definition 1: Polar Decomposition

If $\mathbf X = \mathbf U \mathbf \Sigma \mathbf V^\top$ is the singular value decomposition (SVD) of a matrix, then $\operatorname{polar}(\mathbf X) = \mathbf U \mathbf V^\top$.

Since $\operatorname{polar}(\mathbf X)$ is expensive to compute exactly, Muon uses the Newton-Schulz method to approximate it. Newton-Schulz is an iterative method based on matrix polynomials. Beginning with $\mathbf X_0$, each iteration improves the approximation $\mathbf X_t \approx \operatorname{polar}(\mathbf X)$ according to the update rule

We can interpret Newton-Schulz by understanding how it affects the singular value decomposition.

Let $\mathbf X_0 = \mathbf U \mathbf \Sigma \mathbf V^\top$ be the SVD. Recall that $\mathbf U$ and $\mathbf V$ have orthonormal columns, such that $\mathbf U^\top \mathbf U = \mathbf V^\top \mathbf V = \mathbf I$, and $\mathbf \Sigma$ is a diagonal matrix whose entries are called the singular values. Then

By the same logic,

where we have defined the polynomial $p_1(x) = a_1 x + b_1 x^3 + c_1 x^5$. Since $\mathbf U$ and $\mathbf V$ have orthonormal columns and $p_1(\mathbf \Sigma)$ is diagonal, the right-hand side of this equation must be the SVD of $\mathbf X_1$! This shows that $\mathbf X_1$ shares the same singular vectors $\mathbf U$ and $\mathbf V$ as $\mathbf X_0$, and that its singular values are those of $\mathbf X_0$ transformed according to the polynomial $p_1$. By extension, $\mathbf X_T$ also shares the same singular vectors $\mathbf U$ and $\mathbf V$, and its singular values have been transformed according to the composition of polynomials $(p_T \circ \cdots \circ p_1)(\mathbf \Sigma)$. If $(p_T \circ \cdots \circ p_1)(x) \approx 1$ for all singular values, then $(p_T \circ \cdots \circ p_1)(\mathbf \Sigma) \approx \mathbf I$ and so $\mathbf X_T \approx \mathbf U \mathbf V^\top = \operatorname{polar}(\mathbf X_0)$.

All that remains is to find a sequence of odd polynomials for which $(p_T \circ \cdots \circ p_1)(x) \approx 1$ on the singular values. To make this easier, we first normalize the matrix $\mathbf X_0 = \mathbf X / |\mathbf X|_{\mathsf F}$. This ensures that the singular values of $\mathbf X_0$ lie in the interval $[0, 1]$. The developers of Muon identified a sequence of five degree-5 odd polynomials that approximate $1$ for every input on this interval $[0, 1]$, giving a decent approximation to $\operatorname{polar}(\mathbf X)$ for typical inputs $\mathbf X$ in just five iterations.³

A standard implementation of Newton-Schulz looks like this:

Algorithm 1: Standard Newton-Schulz

Input: $\mathbf X \in \mathbb{R}^{n \times m}$, coefficients ${(a_t, b_t, c_t)}_{t=1}^5$

1. $\mathbf X \gets \mathbf X \,/\, (\lVert\mathbf X\rVert_{\mathsf F} + \epsilon)$    // Normalize sing vals to $[0, 1]$. $\epsilon = 10^{-7}$
2. $\mathbf X \gets \texttt{bfloat16}(\mathbf X)$     // Cast to half precision for speed
3. If $m < n$:  $\mathbf X \gets \mathbf X^\top$   // Trick to make $\mathbf X \mathbf X^\top$ cheaper
4. For $t = 1, \ldots, 5$:       // Apply $p_t(\mathbf X)$
5.    $\mathbf A \gets \mathbf X\mathbf X^\top$
6.    $\mathbf B \gets b_t \mathbf A + c_t \mathbf A^2$
7.    $\mathbf X \gets a_t \mathbf X + \mathbf B \mathbf X$
8. If $m < n$:  $\mathbf X \gets \mathbf X^\top$   // Undo trick
9. Return $\mathbf X$

Successive work has sought to improve Muon in several ways. Most of these proposals modify Muon’s update rule so as to reach the same loss in fewer training steps; however, they use the same Newton-Schulz routine described above. Some methods (e.g., Polar Express) do address Newton-Schulz by changing the sequence of polynomials or the normalization step.¹²¹³ While they improve its approximation accuracy, they do not change its wall-clock runtime. The Dion optimizer⁴ reduces the runtime in the distributed setting, when weights and gradients are sharded across different GPUs. It uses a low-rank approximation of Muon to reduce the communication cost and the dimension of $\mathbf X$, but each step still calls the standard Newton-Schulz routine.

In contrast, our work speeds up Newton-Schulz itself. Since Gram Newton-Schulz is mathematically identical to the standard version, it is compatible with nearly all varieties of Muon.

Runtime of Standard Newton-Schulz

Let’s analyze the runtime of Newton-Schulz in FLOPs to help us understand its performance bottlenekcs. We count only the cubic-time matrix multiplication operations, ignoring the lower-order scalar multiplications and matrix additions. For clarity, we let $T$ denote the number of iterations, remembering that within Muon, $T=5$.¹⁴ We also assume without loss of generality that $n \leq m$ and define the aspect ratio $\alpha = m / n \geq 1$. Intuitively, $\alpha$ measures how rectangular the shape of the matrix is, with $\alpha = 1$ being square and $\alpha \gg 1$ being very rectangular.

Each iteration has three steps. Each step contains a single matrix multiplication costing, respectively,

• $\mathbf X \mathbf X^\top$: $2mn^2$
• $\mathbf A^2$: $2n^3$
• $\mathbf B \mathbf X$: $2mn^2$

for a total cost of $T(4mn^2 + 2n^3) = 2T(2\alpha + 1)n^3$ FLOPs. When $T=5$, the cost is $(20\alpha + 10)n^3$ spread across 15 GEMMs. This analysis highlights two shortcomings of standard Newton-Schulz that inspire our work:

Symmetric Matrix Multiplication

The matrices $\mathbf A = \mathbf X \mathbf X^\top$ and $\mathbf B = b_t \mathbf A + c_t \mathbf A^2$ computed at each iteration of Newton-Schulz are symmetric by definition. This fact can be exploited to reduce the cost of Newton-Schulz. Instead of calling general matrix multiplication routines as typical implementations of Newton-Schulz do, we can compute the lower triangular part of these matrices in the usual way and then simply copy the results to the upper triangular part. This technique halves the cost of computing $\mathbf X \mathbf X^\top$ and $\mathbf A^2$, giving an overall total of $T(3\alpha + 1)n^3$ FLOPs. We describe our custom CuTeDSL kernels that implement this technique below.

Dependence on $\alpha$

Even using symmetric GEMMs, Newton-Schulz’s runtime is dominated by the large rectangular matrix multiplications needed to compute $\mathbf A$ and $\mathbf X$, which together cost $3\alpha n^3$ FLOPs per iteration. A typical implementation with $T=5$ requires 10 of these expensive rectangular multiplications.

This strong dependence on $\alpha$ is unfortunate. Most of the weight matrices in transformer architectures are rectangular, including the MLP weights, MoE weights, and attention projection weights when using GQA or MLA.¹⁵ Furthermore, we observe that the latest MoE architectures are trending towards finer-grained, sparser experts, meaning that the aspect ratios of their hidden dimensions to intermediate dimensions are increasing as well.^1161718

Thus, at large scales, pretraining time would benefit greatly from an algorithm that uses fewer rectangular multiplications and more small symmetric ones.

Gram Newton-Schulz

We now show how to rewrite Newton-Schulz to reduce the number of expensive rectangular matrix multiplications by iterating on the small, square, symmetric Gram matrix $\mathbf X \mathbf X^\top$ instead of the rectangular input matrix $\mathbf X$. The output of this algorithm is mathematically identical to that of standard Newton-Schulz, but it is significantly cheaper to compute.

At a high level, our strategy is based on the following formula. If $\mathbf X \in \mathbb{R}^{n \times m}$ with $n \leq m$, then $\mathrm{polar}(\mathbf X) = (\mathbf X \mathbf X^\top)^{-1/2} \mathbf X$. Rather than use an iterative method to approximate $\mathbf X_T \approx \mathrm{polar}(\mathbf X)$ directly, we instead

1. Compute the $n \times n$ Gram matrix $\mathbf X \mathbf X^\top$
2. Use an iterative method to approximate $\mathbf Q_T \approx (\mathbf X \mathbf X^\top)^{-1/2}$
3. Compute $\mathbf Q_T \mathbf X$

Step 2—which comprises almost all of the algorithm’s wall clock runtime and FLOP cost—works entirely with small $n \times n$ symmetric matrices. This version uses just two rectangular matrix multiplications: $\mathbf X \mathbf X^\top$ in the beginning, and $\mathbf Q_T \mathbf X$ at the end. It also synergizes well with our symmetric GEMM kernels. Because we now use more symmetric multiplications, our kernels provide an even greater speedup than before. Since this method works on the $n \times n$ Gram matrix of $\mathbf X$, we call it “Gram Newton-Schulz”.

How can we turn an iterative polynomial method $(p_T \circ \cdots \circ p_1)(\mathbf X) \approx \operatorname{polar}(\mathbf X)$ like Newton-Schulz into an iterative polynomial method for approximating $\mathbf Y \mapsto \mathbf Y^{-1/2}$? Recall that each $p_t$ is an odd polynomial $p(x) = ax + bx^3 + cx^5$. Any odd polynomial can be rewritten in the form $p(x) = xh(x^2)$, where $h$ is a lower-degree polynomial with the same coefficients, like $h(x) = a + bx + cx^2$. Intuitively, if $p(x) \approx 1$, then $h(y) = p(y^{1/2})y^{-1/2} \approx y^{-1/2}$, so the Newton-Schulz polynomials implicitly provide a way to approximate inverse square roots.

Formally, Gram Newton-Schulz is based on the following theorem. In effect, it shows how to compute $\mathbf X_T$ from $\mathbf X_0$ without ever constructing the intermediate values $\mathbf X_1, \ldots, \mathbf X_{T-1}$:

Theorem 1:

If $p_t(x) = xh_t(x^2)$ for all $t \in {1, \ldots, T}$, then $(p_T \circ \cdots \circ p_1)(x) = q_T x$, where $q_T$ is defined by the iteration $r_0 = x^2$, $q_0 = 1$, and

\[z_t = h_t(r_{t-1})\] \[r_t = r_{t-1}z_t^2\] \[q_t = q_{t-1}z_t\]

for all $t \in {1, \ldots, T}$.

Proof. Define $x_0 = x$ and $x_t = p_t(x_{t-1})$ for $t \in {1, \ldots, T}$. We will show by induction that $r_t = x_t^2$ and $q_t = x_t / x_0$ for all $t$. The base case $t = 0$ holds by the definition $r_0 = x^2, q_0 = 1$. Now assume the hypothesis holds for $t-1$. By assumption,

Observe that $h_t(x_{t-1}^2) = h_t(r_{t-1}) = z_t$, so $x_t = x_{t-1} z_t$. Squaring both sides,

If we instead divide both sides by $x_0$,

Thus, the hypothesis holds for $t$ as well. Finally, observe that $(p_T \circ \cdots \circ p_1)(x) = x_T = q_T x_0$.$\blacksquare$

Note that, as an immediate corollary of the proof, $q_t = x_t / x_0 \to 1/x_0 = \left(x_0^2\right)^{-1/2} = r_0^{-1/2}$. In effect, this shows that $\mathbf Q_T \to (\mathbf X \mathbf X^\top)^{-1/2}$.

To obtain our initial version of Gram Newton-Schulz, we simply lift the iteration from Theorem 1 to matrices. As in standard Newton-Schulz, each matrix operation preserves singular vectors. Therefore, each singular value of $\mathbf R_t$, $\mathbf Q_t$, and $\mathbf Z_t$ evolves independently of the others according to the scalar iteration described above. Note that while this algorithm is mathematically equivalent to standard Newton-Schulz, it is not yet practical due to numerical instability. The only difference between our proposed method and this naive version is the presence of what we call a “restart” at the beginning of iteration 3 of the loop. We will motivate this modification soon.

Algorithm 2: Naive Gram Newton-Schulz

Input: $\mathbf X \in \mathbb{R}^{n \times m}$ with $n \leq m$, coefficients ${(a_t, b_t, c_t)}_{t=1}^5$

1. $\mathbf X \gets \mathbf X \,/\, (\lVert\mathbf X\rVert_{\mathsf F} + \epsilon)$    // Normalize sing vals to $[0, 1]$. $\epsilon = 10^{-7}$
2. $\mathbf R_0 = \mathbf X \mathbf X^\top$
3. $\mathbf Q_0 = \mathbf I$
4. For $t = 1, \ldots, 5$:
5.    $\mathbf Z_t \gets a_t\mathbf I + b_t \mathbf R_{t-1} + c_t \mathbf R_{t-1}^2$    // Apply $h_t(\mathbf R_{t-1})$
6.    $\mathbf Q_t \gets \mathbf Q_{t-1} \mathbf Z_t$
7.    $\mathbf R_t \gets \mathbf Z_t \mathbf R_{t-1} \mathbf Z_t$
8. Return $\mathbf Q_5 \mathbf X$

Gram Newton-Schulz is closely akin to a method proposed in Appendix F of the Polar Express paper.¹² Both form the Gram matrix and transform standard Newton-Schulz into an iteration on $n \times n$ matrices. Both aim to reduce the FLOP cost of Newton-Schulz. However, our work supersedes the proposal from Appendix F in several ways. First, the precise formulas of Gram Newton-Schulz are different, and we believe more stable. Second, we use symmetric matrix multiplication kernels; the opportunity to use these kernels more is an essential advantage of Gram Newton-Schulz not studied previously, and using symmetric matrix multiplication can have subtly different numerical properties in half-precision that require more careful stability strategies. Third, we undertake a thorough stability analysis and provide practical recommendations that allow Gram Newton-Schulz to be used in practice with minimal ad-hoc hyperparameter tuning.

Runtime of Naive Gram Newton-Schulz

Let’s measure the FLOP count of this new algorithm to see how its runtime improves on standard Newton-Schulz. There are four matrix multiplications per iteration. If we use our symmetric GEMM kernel, these cost:

• $\mathbf R_{t-1}^2$: $n^3$
• $\mathbf Q_{t-1} \mathbf X_t$: $n^3$
• $\mathbf Z_t \mathbf R_{t-1} \mathbf Z_t$: $n^3 + n^3$

The initialization and output steps cost:

• $\mathbf X \mathbf X^\top$: $mn^2$
• $\mathbf Q_5 \mathbf X$: $2mn^2$ (not symmetric)

Lastly, computing $\mathbf Q_1 = \mathbf Z_1$ is free since $\mathbf Q_0 = \mathbf I$, and we do not need to compute $\mathbf R_5$:

• Skipping $\mathbf Q_0 \mathbf Z_1,\,\mathbf Z_5 \mathbf R_4 \mathbf Z_5$: $-3n^3$

Thus, the total FLOP count is $T\cdot4n^3 + 3mn^2 - 3n^3 = (4T + 3\alpha - 3)n^3$ for general $T$, or $(17 + 3\alpha)n^3$ across 19 GEMMs for $T=5$. Compare this to standard Newton-Schulz’s $T(3\alpha + 1)n^3$ FLOPs when using symmetric GEMMs. When $\alpha = 1$, they are equal. When $\alpha > 1$, Gram Newton-Schulz is cheaper. For a typical Muon application ($T=5, \alpha = 4$), it saves 55% of the FLOPs used by standard Newton-Schulz with symmetric GEMMs, or 68% compared to a typical implementation without symmetric GEMMs.

In practice, when $\alpha=1$, we fall back to standard Newton-Schulz with our symmetric GEMMs, since it launches fewer GEMMs and will have a faster wall clock time.

Instability of Naive Gram Newton-Schulz

Let’s try training a transformer LLM with Muon using Naive Gram Newton-Schulz:

 _Figure 2: Naive Gram Newton-Schulz on Llama-430M.

This is no good. Not only do we get loss spikes, but eventually, the output of Gram Newton-Schulz is full of Infs! While Gram Newton-Schulz is mathematically equivalent to standard Newton-Schulz in exact arithmetic, it behaves differently in finite precision, especially in half precision.

We will now pause to explain the source of this instability in detail and motivate our solution. Readers not concerned with these technical details can skip ahead to see the stabilized method. Code for running these stability experiments and generating the figures is available here.

Tracking Eigenvalues of Intermediate Matrices

We can understand how matrices evolve and why they diverge by studying their eigenvalues and singular values. Recall that the entries of any matrix are upper bounded by its largest singular value, so if we control the singular values, we will prevent blowups.

If $\mathbf X = \mathbf U \mathbf \Sigma \mathbf V^\top$ is the SVD of the input matrix, then intermediate matrices of Algorithm 2 ($\mathbf R_t$, $\mathbf Q_t$, $\mathbf Z_t$) are square symmetric with eigenvectors $\mathbf V$. In exact arithmetic, $\mathbf U^\top \mathbf R_t \mathbf U$ is a diagonal matrix containing $\mathbf R_t$’s eigenvalues, each of which corresponds to a singular value of $\mathbf X$. We can therefore plot the eigenvalues of $\mathbf R_t$ and $\mathbf Q_t$ against the corresponding singular values of $\mathbf X$ to track how each evolves according to the polynomial update rules—or diverges from them.

To see how things should look, let’s start by running Naive Gram Newton-Schulz in full float64 precision for $10$ steps. We will use a synthetic input—a $128 \times 512$ matrix with an exponentially decaying spectrum. In order to make our plots more readable, with smooth monotonic curves, the experiments in this section use the coefficients $(a_t, b_t, c_t) = (\tfrac{15}8, \tfrac{10}8, \tfrac38)$ at every iteration. The numerical behavior we observe will generalize to other coefficients; those used in practice (like You Jiacheng’s or Polar Express) will blow up at an even earlier iteration, matching the behavior we observe in training.¹⁹¹² Even though our method does not need to compute the intermediate matrices $\mathbf X_1, \ldots, \mathbf X_{T-1}$, we do so here for demonstration using the formula $\mathbf X_t = \mathbf Q_t \mathbf X_0$, where we label the input $\mathbf X_0$ for clarity.

 _Figure 3: Evolution of eigenvalues of $\mathbf R_t$, $\mathbf Q_t$, and $\mathbf X_t$ in Float64 in Naive Gram Newton-Schulz with coefficients $(\tfrac{15}8, \tfrac{10}8, \tfrac38)$.

Initially, we have $r_0 = x_0^2$, and $q_0 = 1$. As the algorithm proceeds, we know that $x_t \to 1$, so we expect $r_t \to 1$ and $q_t = x_t / x_0 \to 1/x_0 = r_0^{-1/2}$ as per Theorem 1. Note that if $x_0$ is close to 1, the method converges quickly, while if $x_0$ is close to zero, it converges slowly. After 10 iterations, the spectrum of $\mathbf X_t$ is visually indistinguishable from $1$, as expected.

Now let’s repeat the experiment using bfloat16 instead of float64 arithmetic:

 _Figure 4: Evolution of eigenvalues of $\mathbf R_t$, $\mathbf Q_t$, and $\mathbf X_t$ in BFloat16 in Naive Gram Newton-Schulz with coefficients $(\tfrac{15}8, \tfrac{10}8, \tfrac38)$.

The first few iterations proceed as before. However, by step 7, we see unexpected behavior in the spectrum of $\mathbf X_t$. The singular values that began near $0$ suddenly jump up above 1, instead of converging to 1 from below. By step 8, the algorithm is returning complete junk. What happened?

We identify two key causes of divergence:

1. Spurious negative eigenvalues of the Gram matrix $\mathbf X \mathbf X^\top$
2. Eigenvector drift

Spurious Negative Eigenvalues

The main cause of divergence is the presence of negative eigenvalues in the Gram matrix due to half-precision arithmetic. These negative eigenvalues blow up after a few iterations of Gram Newton-Schulz.

If you look closely, you can see that the trouble begins in $\mathbf R_t$. By construction, $r_t = x_t^2 \geq 0$, so in exact arithmetic, $\mathbf R_t$ should be a positive semidefinite matrix. However, when using bfloat16, our plots show that $\mathbf R_t$ has negative eigenvalues! Because $\mathbf X_0$ is numerically low rank, $\mathbf R_0 = \mathbf X_0 \mathbf X_0^\top$ has eigenvalues that are numerically equal to zero, and in bfloat16, a number like $-10^{-5}$ is numerically equal to zero. Let’s transform the y-axis to emphasize values close to zero and replot this:

 _Figure 5: Evolution of eigenvalues of $\mathbf R_t$, $\mathbf Q_t$, and $\mathbf X_t$ in BFloat16, with y-axis centered around $0$.

Now we see that from the very beginning, $\mathbf R_0$ has tiny negative eigenvalues introduced in the first computation $\mathbf X_0 \mathbf X_0^\top$. Later computations can introduce additional negative eigenvalues to $\mathbf R_t$ too. These eigenvalues represent nothing about the original problem, they are just an artifact of floating point arithmetic. Therefore, we call them “spurious eigenvalues”.

These spurious negative eigenvalues start small, but the plot shows that their magnitude grows quickly. Let’s understand mathematically why this happens. Recall the update rule: \(r_t = r_{t-1} z_t^2 = r_{t-1} h_t(r_{t-1})^2\) If we now substitute $h_t(x) = \tfrac{15}8 - \tfrac{10}8 x + \tfrac38 x^2$ and plot this update rule, we can see the problem:

Figure 6: Negative values of $r_t$ diverge towards negative infinity.

As the plot shows, $r_t < \left(\tfrac{15}{8}\right)^2 r_{t-1}$. Thus, if $r_0 < 0$, the magnitude of the spurious eigenvalues grows exponentially! This sets off a chain reaction. As $r_t \to -\infty$, we get $z_t \to \infty$. This causes $q_t \to \infty$ and therefore also $x_t \to \infty$. This problem cannot be fixed by choosing different polynomials. Conceptually, in the main loop, we are attempting to compute the inverse square root of a negative number. It cannot help but diverge.

To show that the spurious negative eigenvalues of $\mathbf R_0$ are enough to cause this catastrophic failure, let’s rerun the method with every operation in float64 precision, except that we will convert $\mathbf R_0$ from float64 to bfloat16 and then back to float64 to induce a little floating point error. As you can see, even this causes a blowup.

 _Figure 7: Evolution of eigenvalues of $\mathbf R_t$, $\mathbf Q_t$, and $\mathbf X_t$ when all operations use Float64 except $\mathbf R_0 = \mathbf X \mathbf X^\top$.

Recall that the average magnitude of a matrix’s entries (root mean squared) is proportional to its Frobenius norm, which is larger than the largest singular value. Therefore, as $\mathbf Q_t$’s largest singular value blows up, its entries do too.

Eigenvector Drift

Spurious negative eigenvalues are not the only source of instability. If we take as input a matrix that excludes small singular values (i.e., all $\geq 0.017$), then we do not observe any negative eigenvalues in $\mathbf R_t$, but we still see a moderate blow up in $\mathbf X_t$. The culprit seems to be eigenvector drift.

In exact arithmetic, the eigenvectors of all intermediate matrices match $\mathbf U$, the left singular vectors of $\mathbf X_0$, but in finite precision they do not. This effect can be measured by observing how far $\mathbf U^\top \mathbf R_t \mathbf U$, $\mathbf U^\top \mathbf Q_t \mathbf U$, and $\mathbf U^\top \mathbf X_t \mathbf V$ are from being diagonal matrices. The plot below shows that after several iterations, the eigenvectors of $\mathbf Q_t$ and $\mathbf X_t$ have drifted significantly. At the same time, we see the eigenvalues of $\mathbf Q_t$ (and by extension, those of $\mathbf X_t$) diverge from where they should be in exact arithmetic. The growing eigenvalues of $\mathbf Q_t$ seem to spill into one another. The strength of this effect is less consistent than that of negative eigenvalues, but it is still harmful.

Figure 8: As the eigenvectors drift (left) the spectral norms of $\mathbf R_t$, $\mathbf Q_t$, and $\mathbf X_t$ diverge.

Stabilizing Gram Newton-Schulz by Restarting

If we run Gram Newton-Schulz for more than a few iterations, the spurious negative eigenvalues grow unmanageably large and $\mathbf Q_t$ blows up. Our solution is simple: run Gram Newton-Schulz for only a few iterations. Rather than using Gram Newton-Schulz to compute $\mathbf X_T$ directly, we use it to compute, say, $\mathbf X_5$ in a stable manner for coefficients $(\tfrac{15}8, \tfrac{10}8, \tfrac38)$. While $\mathbf X_5$ is not a good approximation to $\lim_{T \to \infty} \mathbf X_T = \mathrm{polar}(\mathbf X_0)$, we are closer than when we started. Now we can apply Gram Newton-Schulz a second time on the input $\mathbf X_5$ to compute $\mathbf X_{10}$ stably. We can repeat this over and over to reach whatever $T$ we like. This restarting technique sacrifices some of the performance gains of Gram Newton-Schulz, but it still offers a significant speedup over standard Newton-Schulz.

Below we plot the results of this method on the same test matrix used above. As before, we compute $\mathbf X_t$ for all $t$ for diagnostic purposes, though the algorithm computes only $\mathbf X_5, \mathbf X_{10}, \ldots, \mathbf X_{30}$. Looking closely, you can see that $\mathbf R_t$ develops some negative eigenvalues, but unlike before, the growth of these eigenvalues is controlled. Each time we restart, we re-initialize $\mathbf R_t = \mathbf X_t \mathbf X_t^\top$, eliminating any negative eigenvalues of large magnitude. As you can see, at iteration $5, 10, 20, 25$, and $30$, $\mathbf Q_t$ resets to the identity. Therefore, the eigenvalues of $\mathbf Q_t$ never grow beyond $\approx 12$, despite the negative eigenvalues in $\mathbf R_t$. Since the eigenvalues of $\mathbf Q_t$ remain controlled, those of $\mathbf X_t = \mathbf Q_t \mathbf X_{t-5}$ stay strictly smaller than $1$.

 _Figure 9: Restarting prevents the divergence of $\mathbf R_t$.

Restarting also helps control eigenvector drift. We repeat the experiment from above on the same matrix (with all singular values $> 0.017$), but now with a restart after step 5. We observe that the diagonalization error remains $\leq 0.05$ for all matrices, and the maximum eigenvalues now align closely with their values in exact arithmetic. Note that we always measure eigenvector drift relative to the original input $\mathbf X_0$, not the restarted $\mathbf X_5$.

 _Figure 10: Restarting prevents eigenvector drift.

When to Restart: Polar Express Coefficients for Muon

At what iteration should we restart? To avoid numerical trouble, we need to control the magnitude of $\mathbf Q_t$, even when $\mathbf R_0$ has spurious negative eigenvalues. (Because each $q_r \geq 1$, this is equivalent to controlling the condition number of $\mathbf Q_t$.) So long as each eigenvalue of $\mathbf Q_t$ remains smaller than the inverse of the corresponding eigenvalue from $\mathbf X$, then $\mathbf X_t = \mathbf Q_t \mathbf X$ will have eigenvalues $\leq 1$.

The growth of $\mathbf Q_t$ in turn depends on the size of the spurious negative eigenvalues and the specific sequence of polynomials we use. Furthermore, since the polynomial $p_t$ changes at each iteration, it may not be ideal to restart at regular intervals. Instead, we can choose when to restart adaptively, depending on the specific sequence of polynomials we have applied since the previous restart.

For the application to Muon, let’s now switch over to using five iterations of the Polar Express polynomials, which are defined as follows:

In the example above, we observe that the most negative spurious eigenvalue of $\mathbf R_0$ is about $-4 \cdot 10^{-4}$. Using the scalar analogue Gram Newton-Schulz, let’s simulate how the eigenvalues of $\mathbf Q_t$ evolve in full precision when $\mathbf R_0$ has eigenvalues in the range $[-4\cdot 10^{-4}, 1]$. With no restart, they blow up:

Figure 11: Min/max eigenvalue of $\mathbf R_t$ and $\mathbf Q_t$ without restarts. $\mathbf R_0$ starts with a negative eigenvalue as low as $-4 \times 10^{-4}$.

Now let’s repeat the experiment with a restarted version of the algorithm. To obtain a good balance of stability and speed, let’s limit ourselves to a single restart. When should this restart take place? We’ll try all possibilities. As above, we begin with eigenvalues in the range $[-4 \cdot 10^{-4}, 1]$. Every time we restart and form $\mathbf R = \mathbf X\mathbf X^\top$, we subtract $4 \times 10^{-4}\mathbf I$ to simulate a potentially dangerous shift in the eigenvalues due to floating point error. As you can see, restarting after the second iteration ensures that the eigenvalues of $\mathbf R_t$ stay well above $-0.4$ and that the condition number of $\mathbf Q_t$ stay below $\approx 100$ for all iterations, much better than the other options.

Figure 12: Minimum eigenvalue of $\mathbf R_t$ and condition number of $\mathbf Q_t$ if restart is placed after iteration $1$, $2$, $3$, or $4$. $\mathbf R_0$ starts with a negative eigenvalue as low as $-4 \times 10^{-4}$. Restarting after iteration $2$ provides the best bound on $\mathbf Q_t$.

Note that restarting works precisely because we reset the minimum negative eigenvalue of $\mathbf R_t$, which in turn tightens the bound on $\mathbf Q_t$’s eigenvalues. In our repo, we provide a utility that performs this analysis. For any given Newton-Schulz coefficients and any number of restarts, it identifies the best iterations at which to restart.

Now let’s run the full method with a restart after the second iteration on our test matrix. Now it converges! All singular values of $\mathbf X_t$ approach 1.

Figure 13: Restarting after $2$ iterations creates a stable polar decomposition of our test matrix with Polar Express coefficients.

Further Precautions

While restarting greatly improves stability, it is not absolutely foolproof. The usual numerical snags for Newton-Schulz still apply.

For example, most choices of Newton-Schulz polynomials are designed to converge only when $\lVert\mathbf X_0\rVert \leq 1$; any singular values larger than $1$ may diverge rapidly.

Figure 14: Theoretical behavior of both standard and Gram Newton-Schulz on $\sigma{X0}$ slightly above $1$ using Polar Express coefficients.

Even with a properly normalized input, perturbed singular values of $\mathbf X_0$ slightly greater than $1$ can develop due to numerical error. This problem affects standard Newton-Schulz as well, so the Polar Express polynomials are typically adjusted according to the formula $\tilde p_t(x) = p_t(x / 1.02)$. This ensures convergence even for singular values as large as $1.02$. When using Gram Newton-Schulz, roundoff errors like this can worsen due to computations like $\mathbf X\mathbf X^\top$, which do not have built-in safety factors; however, we have never seen this happen when using our recommended setup (float16 arithmetic with restarting after $2$ iterations). It is generally wise to be extra conservative in the choice of safety factor, for instance, by replacing $1.02$ with $1.05$.

Float16 vs BFloat16 in Newton-Schulz

In addition, we argue for using float16 instead of bfloat16 to implement Newton-Schulz. Compared to bfloat16, float16 can only represent values from a narrower range, but it has greater precision within that range. For our purposes, the range of float16 (roughly $6.1\cdot 10^{-5}$ to $6.5 \cdot 10^4$) suffices because the magnitudes of our matrices are controlled to lie near 1. And in some cases, we can benefit from using float16 to reduce numerical errors.

On certain test matrices, we see more accurate $\operatorname{polar}(\mathbf X)$ approximations with float16, but in practice, we have not found a case where the pretraining loss is meaningfully different between float16 and bfloat16. Still, we default to float16.

Computing Matrix Quadratics

A key step in Gram Newton-Schulz is computing the matrix quadratic $\mathbf Z_t \gets a_t\mathbf I + b_t \mathbf R_{t-1} + c_t \mathbf R_{t-1}^2$. PyTorch implementations of Newton-Schulz typically do not assemble such polynomials explicitly; to compute $\mathbf X(\mathbf a_t \mathbf I + b_t \mathbf A + c_t \mathbf A^2)$, they partly distribute $\mathbf X$ and use two calls to torch.baddbmm, which dispatches to cuBLAS GEMM, as follows

1.    $\mathbf B \gets b_t \mathbf A + c_t \mathbf A^2$
2.    $\mathbf X \gets a_t \mathbf X + \mathbf B \mathbf X$

Our symmetric GEMM kernel is capable of fusing these matrix quadratics into a single step. In particular, it can fuse the addition of $\gamma \mathbf I$ by adding $\gamma$ to all diagonal entries of the output when they are at the register level. This optimization completely obviates any I/O operations needed for the $\gamma I$ addition, typically outspeeding gemm_symmetric(A, B, C, alpha, beta) + gamma * I, which would require loading $\mathbf I$ from general memory to shared memory to registers. Once $\mathbf Z_t$ is assembled, Gram Newton-Schulz can use it in three subsequent multiplications.

However, our tests show that adding $\gamma \mathbf I$ explicitly can be less stable than handling it implicitly in some corner cases. If we stress-test our method by ignoring some of our own advice—restarting after three iterations instead of two and using a Polar Express safety factor of $1.02$ instead of $1.05$, and computing the quadratic with $a_t \mathbf I$ explicitly—then we observe instability. This instability disappears if we use non-symmetric GEMMs (either from torch or Quack) instead of our symmetric kernels. We conclude that our fused quadratic kernel can hurt stability in this setting. Since we reproduce this issue by forcing symmetry after calling standard torch GEMMs, we know this is not a kernel bug, but a numerical property.

We believe this effect can be explained as follows. While the fused kernel computes $a_t\mathbf I + b_t \mathbf R_{t-1} + c_t \mathbf R_{t-1}^2$ in float32 arithmetic under the hood, the result $\mathbf Z_t$ is rounded back down to float16 at the end of the GEMM. Future computations like $\mathbf Q_t \mathbf Z_t$ suffer from this loss of precision in $a_t$. In contrast, if the $a_t \mathbf I$ term is handled implicitly, all arithmetic involving $a_t$ takes place in float32. Therefore, it is more accurate to compute $a_t \mathbf Q_t + \mathbf Q_t\left(b_t \mathbf R_{t-1} + c_t \mathbf R_{t-1}^2\right)$ than $\mathbf Q_t\left(a_t\mathbf I + b_t \mathbf R_{t-1} + c_t \mathbf R_{t-1}^2\right)$.

We reiterate that in all our experiments, this instability can be avoided entirely by restarting correctly or by using a higher safety factor of $1.05$. Out of an abundance of caution, we rearrange the arithmetic of Naive Gram Newton-Schulz to avoid adding $\mathbf I$ explicitly. That is, we change

1.    $\mathbf Z_t \gets a_t\mathbf I + b_t \mathbf R_{t-1} + c_t \mathbf R_{t-1}^2$    // Apply $h_t(\mathbf R_{t-1})$
2.    $\mathbf Q_t \gets \mathbf Q_{t-1} \mathbf Z_t$
3.    \((\mathbf{RZ})_t \gets \mathbf R_{t-1} \mathbf Z_t\)
4.    \(\mathbf R_t \gets \mathbf Z_t (\mathbf{RZ})_t\)

to

1.    $\mathbf Z_t \gets b_t \mathbf R_{t-1} + c_t \mathbf R_{t-1}^2$
2.    $\mathbf Q_t \gets \mathbf Q_{t-1} \mathbf Z_t + a_t\mathbf Q_{t-1}$
3.    \((\mathbf{RZ})_t \gets \mathbf R_{t-1} \mathbf Z_t + a_t\mathbf R_{t-1}\)
4.    \(\mathbf R_t \gets \mathbf Z_t (\mathbf{RZ})_t + a_t(\mathbf{RZ})_t\)

This change fixes all collected examples in which symmetric GEMMs were less stable than non-symmetric GEMMs.

Takeaways on Stability

While Gram Newton-Schulz is fundamentally more unstable than standard Newton-Schulz, it can be coaxed into behaving equally stably with the proper care. The understanding gleaned from these experiments gives us the confidence to use Gram Newton-Schulz in practice. However, users should be willing to monitor the method, and if they find instability, to adjust the hyperparameters (e.g., $1.02 \to 1.05$ above). For example, a second restart may be required if using a particularly sensitive set of coefficients or if running more than five iterations with Polar Express polynomials.

In the application of Muon for pretraining, we do not need very high polar decomposition accuracy, and our experiments below show that Muon with Gram Newton-Schulz yields effectively identical results to Muon with standard Newton-Schulz in terms of training quality. However, when high accuracy is desired, the usual warnings about forming the Gram matrix apply. Since forming $\mathbf X \mathbf X^\top$ immediately squares the condition number, Gram Newton-Schulz may not be appropriate in these cases.

Stabilized Gram Newton-Schulz

We now present our complete algorithm, which enjoys the speed of naive Gram Newton-Schulz while remaining numerically stable. We use five iterations of Newton-Schulz with degree-5 polynomials (such as Polar Express). We use float16 arithmetic, and we “restart” after the first two iterations by setting $\mathbf X \gets \mathbf Q_2 \mathbf X$ and reinitializing $\mathbf R_2$ and $\mathbf Q_2$. As in standard Newton-Schulz, we write the logic of our routine assuming that $\mathbf X$ has more columns than rows. If this is not the case, we simply run on $\mathbf X^\top$ and output the transpose of the result.

Algorithm 3: Stabilized Gram Newton-Schulz

Input: $\mathbf X \in \mathbb{R}^{n \times m}$ with $n \leq m$, coefficients ${(a_t, b_t, c_t)}_{t=1}^5$

1. $\mathbf X \gets \mathbf X \,/\, (\lVert\mathbf X\rVert_{\mathsf F} + \epsilon)$    // Normalize sing vals to $[0, 1]$. $\epsilon = 10^{-7}$
2. $\mathbf X \gets \texttt{float16}(\mathbf X)$     // Cast to half precision for speed
3. If $m < n$:  $\mathbf X \gets \mathbf X^\top$   // Trick to make $\mathbf X \mathbf X^\top$ cheaper
4. $\mathbf R_{0} \gets \mathbf X \mathbf X^\top$
5. $\mathbf Q_{0} \gets \mathbf I$
6. For $t = 1, \ldots, 5$:
7.    If $t = 3$:        // Restart to stabilize
8.      $\mathbf X \gets \mathbf Q_2 \mathbf X$
9.      $\mathbf R_2 \gets \mathbf X \mathbf X^\top$
10.      $\mathbf Q_2 \gets \mathbf I$
11.    $\mathbf Z_t \gets b_t \mathbf R_{t-1} + c_t \mathbf R_{t-1}^2$
12.    $\mathbf Q_t \gets \mathbf Q_{t-1} \mathbf Z_t + a_t\mathbf Q_{t-1}$
13.    \((\mathbf{RZ})_t \gets \mathbf R_{t-1} \mathbf Z_t + a_t\mathbf R_{t-1}\)
14.    \(\mathbf R_t \gets \mathbf Z_t (\mathbf{RZ})_t + a_t(\mathbf{RZ})_t\)
15. $\mathbf X \gets \mathbf Q_4 \mathbf X$
16. If $m < n$:  $\mathbf X \gets \mathbf X^\top$  // Undo trick
17. Return $\mathbf X$

Runtime of Stabilized Gram Newton-Schulz

Above, we showed that Naive Gram Newton-Schulz uses $(4T + 3\alpha - 3)n^3$ FLOPs. How does restarting change this? It requires two additional matrix multiplications:

• $\mathbf X \gets \mathbf Q_2 \mathbf X$: $2mn^2$
• $\mathbf R_2 \gets \mathbf X \mathbf X^\top$: $mn^2$

Since the initial value of $\mathbf R_2$ is discarded and $\mathbf Q_2 = \mathbf I$, it also allows us to skip three matrix multiplications:

• $\mathbf R_2 \gets \mathbf Z_2 \mathbf R_1\mathbf Z_2$: $-n^3 - n^3$
• $\mathbf Q_3 \gets \mathbf Q_2 \mathbf Z_3$: $-n^3$

Therefore, Stabilized Gram Newton-Schulz with one restart uses $(4T + 6\alpha - 6)n^3$ FLOPs. As before, this matches standard Newton-Schulz for $\alpha = 1$ and improves on it for $\alpha > 1$. For $T=5, \alpha = 4$, our algorithm reduces the number of FLOPs by 42% compared to standard Newton-Schulz with symmetric GEMMs, or by 58% compared to typical implementations lacking symmetric GEMMs.

Observe that if we hypothetically used more restarts, each would increase the FLOPs by $3mn^2 - 3n^3$. With $T-1$ restarts, Gram Newton-Schulz would be exactly the same algorithm as standard Newton-Schulz.

In this sense, adding restarts can be viewed as trading wall clock time for greater guaranteed stability, with the extrema being Naive Gram Newton-Schulz and standard Newton-Schulz.

Symmetric GEMM Kernels in CuTeDSL

To take advantage of the greater share of symmetric matrix multiplications enabled by Gram Newton-Schulz, we implement kernels for the operations $\mathbf A \mathbf B$ and $\alpha \mathbf A \mathbf B + \beta \mathbf C$ that assume $\mathbf A \mathbf B$ and $\mathbf C$ are symmetric. Symmetric kernels also accelerate standard Newton-Schulz; this idea has been around for a while for the construction of the Gram $\mathbf{XX^\top}$, but to our knowledge, hasn’t been explored for fused symmetric matrix multiplication with addition.⁹²⁰ We target the Hopper and Blackwell GPU architectures and open source our implementation in the Quack library of CuTeDSL kernels developed by our lab.

Figure 15: SOTA Symmetric GEMM Kernels benchmarked on Hopper and Blackwell against cuBLAS.

Layout Engineering and Work Scheduling

GEMM implementations of $\mathbf A \mathbf B$ and $\alpha \mathbf A \mathbf B + \beta \mathbf C$ can be broken down into the following components:

1. How do we schedule GEMM output tiles as work among groups of workers?
2. Once assigned a tile, how does a group of workers compute the tile?

In most GEMM and fused GEMM kernels, tiles are computed in the same way, with the following components:

1. The prologue, in which rows of $A$ and columns of $B$ needed for the current tile are loaded in from general memory (high-bandwidth memory) to shared memory (SRAM)
2. Matrix-Multiply Accumulate (MMA), in which those rows and columns are multiplied and written to the register file in Hopper or tensor memory in Blackwell
3. The epilogue, in which additional tensors needed for the fusion are loaded in, the fused arithmetic occurs, and the final values are written to the output tensor(s), from the register file to shared to general memory. An example is loading in $C$, $\alpha$, $\beta$, and then scaling $\mathbf A \mathbf B$ with $\alpha$ and adding $\beta \mathbf C$.

Our symmetric GEMM kernel and the standard GEMM kernel only differ in how they schedule and partition output tiles as work and how they implement their epilogues.

Triangular Scheduler

In the standard GEMM, the entire output matrix is divided into work tiles that are load balanced and evenly partitioned amongst clusters of thread blocks, where thread blocks in the same cluster can access the same shared memory and are therefore scheduled to run together. Then, each cluster computes its assigned work tiles in succession.

Our tile scheduler in the symmetric GEMM is almost identical. The only difference is that only the work tiles in the lower triangle of the matrix are partitioned amongst the clusters, and work tiles in the upper triangle are unassigned, since their values are identical to the transposed values of the lower triangle.

Instead of using the standard tile scheduler which evenly divides the tiles of both triangles among the clusters, we use a triangular scheduler to evenly divide only the tiles of only the lower triangle among the clusters. This ensures that every cluster gets assigned the same number of tiles that actually need to be worked on, ensuring load balancing.

Epilogue: Writing to the Transposed Tile

In the GEMM epilogue, when the computed values of the lower triangle are written to their assigned tile in general memory (HBM), they are also written to their transposed tile location in the upper triangle.

Figure 16: Symmetric GEMM only computes $256 \times 256$ work tiles on the diagonal and in the lower triangle, copying and transposing each lower tile to its transposed location in the upper triangle.

We implement all of our symmetric GEMM kernels with square cluster work tiles. Hopper uses cluster size $(2, 1)$ and thread block tile size $(128, 256)$, and Blackwell uses cluster size $(2, 1)$ and 2-CTA collaboration, in which the 2 thread blocks in the cluster collaborate on the same big $(256, 256)$ tile.

Notably, highly optimized custom GEMM kernels on Hopper typically use Ping Pong Scheduling, in which the MMA of tile $i$ and the epilogue of tile $i-1$ are overlapped in two consumer warp groups²¹. However, Ping Pong Scheduling uses more registers at once, and $(128, 256)$ is too large of a tile size for Ping Pong Scheduling, leading to register spillage. This is much slower than standard single producer warp, single consumer warp scheduling. Thus, our Hopper symmetric kernels do not use Ping Pong Scheduling. Blackwell GEMM kernels have no explicit conception of Ping Pong Scheduling, since by default in both cuBLAS and Quack, two accumulators are kept in the new tensor memory hierarchy, and MMA is computed on one accumulator while the epilogue is computed on the other.

As a small implementation detail, note that the main diagonal of $256 \times 256$ cluster work tiles is part of the work assigned by the triangular scheduler. Since their transposed locations are identical to their current locations, we only write those values to general memory once - writing twice can cause inaccurate values or NaN’s.

Implementation Strategy in Code

There are only two differences between the symmetric GEMM kernel and the standard GEMM kernel: the triangular scheduler and the transposed tile write in the epilogue. Quack is designed around abstracting the standard GEMM kernel to enable lightweight but maximally performant GEMM epilogue fusions. Using these abstractions, we are able to implement the symmetric GEMM kernel for both Hopper and Blackwell in just 160 lines, while achieving SOTA performance.

We override the standard tile scheduler with our triangular scheduler and wrap the symmetric GEMM class around the GEMM with activation class. GEMM with activation itself is a wrapper around the Blackwell and Hopper default GEMMs. It supports writing two output tensors - the standard GEMM output (the preactivation) and the standard GEMM output with an activation function such as SwiGLU or ReLU applied (the postactivation). We define the activation function to be the identity and the postactivation tensor to be the inplace transpose of the preactivation tensor. Then, when the GEMM with activation class writes to the postactivation, it is really writing to the upper triangle with a tranposed layout - this is exactly the intent of the symmetric GEMM kernel. We override the epilogue of GEMM with activation just to ensure we don’t write twice to the diagonal tiles, for the correctness reasons mentioned previously.

We’re super excited about this simplicity! Without this abstraction, the initial implementation was close to 1500 lines of CuTeDSL. It shows the convenience of principled abstractions in kernel engineering, specifically that of the GEMM main loop + Epilogue paradigm.²²

Kernel Optimizations for Standard Newton-Schulz

Using just our Quack CuTeDSL kernels, we can accelerate standard Newton-Schulz with two changes.

1. Symmetric Matrix Multiplication As discussed above, the matrices $\mathbf A = \mathbf X \mathbf X^\top$ and $\mathbf B = b_t \mathbf A + c_t \mathbf A^2$ computed at each iteration of Newton-Schulz are symmetric by definition. Therefore, we use our symmetric GEMM kernels for these operations, reducing their FLOP cost by half.
2. Fused GEMM + Add The typical way to implement the non-symmetric multiplication $\mathbf X \gets a_t \mathbf X + \mathbf B \mathbf X$ is to use torch.baddbmm, which calls cuBLAS under the hood. However, Quack offers a much faster implementation of this “Fused GEMM + Add” operation for Hopper. Unlike cuBLAS, Quack supports Ping Pong Scheduling for Hopper, which better hides the epilogue addition of $a_t \mathbf X$.

This table shows that the total runtime of applying standard Newton-Schulz to all weight matrices of various LLMs decreases by about 25\% when combining these kernel optimizations on the Hopper architecture.

Table 1: On Hopper, using symmetric kernels and Ping Pong Scheduling in GEMM + Add accelerates standard Newton-Schulz by around $25\%$ already.

Training Experiments and Benchmarks

We validate Gram Newton-Schulz’s training quality and performance gain on Llama-430M, Qwen-600M, Gemma-1B, and a custom MoE-1B architecture with ~20% active parameters across 1 billion total parameters.²³¹⁷²⁴

We train on FineWeb-Edu. The number of training tokens for each dense model is given by the Chinchilla scaling law and for MoE-1B by twice the Chinchilla scaling law with respect to its active parameters. We use a cosine learning rate scheduler with the following base learning rates:

For both profiling and full training runs, our Muon setup is as follows:

1. Weights orthogonalized by Muon include $\mathbf W_q, \mathbf W_k, \mathbf W_v$ (the projection matrices for attention), $\mathbf W_o$ (the out-projection matrix following attention), $\mathbf W_{MLP_{UP}}$, $\mathbf W_{MLP_{GATE}}$, and $\mathbf W_{MLP_{DOWN}}$ (the SwiGLU MLP weights), and $\mathbf W_{router}$ (the token router matrix for MoE).
2. Each instance of $\mathbf W_q, \mathbf W_k, \mathbf W_v, \mathbf W_o, \mathbf W_{MLP_{UP}}, \mathbf W_{MLP_{GATE}}$, $\mathbf W_{MLP_{DOWN}},$ and $\mathbf W_{router}$ is batched across all transformer layers; that is, we execute a Newton-Schulz call for all the $\mathbf W_q$’s at once, for all the $\mathbf W_k$’s at once, etc. Maximizing the batch size of Newton-Schulz improves efficiency by making the batched GEMM operations as compute-bound as possible.

Muon is generally combined with a learning rate adjustment that scales the effective step size for each weight matrix based on its dimensions. We find that using Moonshot AI’s strategy of scaling the update by $0.2 \sqrt{\max(\mathrm{fan_out}, \mathrm{fan_in})}$—roughly matching the RMS of Muon’s update with that of AdamW—yields the best loss curves.²⁵

Splitting the Weights

We draw special attention to the fact that we split $\mathbf W_{MLP_{UP}}$ from $\mathbf W_{MLP_{GATE}}$ and orthogonalize them separately. Ordinarily, MLPs are implemented as Linear + SwiGlu + Linear, where the weight matrix of the first linear layer is a concatenation of $\mathbf W_{MLP_{UP}}$ and $\mathbf W_{MLP_{GATE}}$. However, the gradients flowing back into the $\mathbf W_{MLP_{UP}}$ and $\mathbf W_{MLP_{GATE}}$ halves are calculated quite differently since their contributions to the activation are fundamentally different. We observe that orthogonalizing them separately improves the final loss; for example, in Llama-430M, we observe an improvement of $\approx 0.2$ in perplexity. In addition, splitting $\mathbf W_{MLP_{UP/GATE}}$ halves its small dimension in MoE architectures, where the intermediate size is smaller than the hidden size, leading to greater speedup from Gram Newton-Schulz.

Likewise, while earlier implementations of Muon orthogonalized the combined matrix $\begin{bmatrix} \mathbf W_q \,\vert\, \mathbf W_k \,\vert\, \mathbf W_v\end{bmatrix}$, we orthogonalize each piece separately.

We are also aware that in some settings, including pretraining GLM-5, Muon benefits from splitting Multi-Latent Attention weights ($\mathbf W^{UQ}$, $\mathbf W^{UK}$, and $\mathbf W^{UV}$) by attention head before orthogonalizing.² This choice is principled, since the actual matrix multiplications happening in attention are between attention heads rather than the full query, key, value, and out projections. On our test models, we experimented with splitting $\mathbf W_q$, $\mathbf W_k$, $\mathbf W_v$, and $\mathbf W_o$ by attention heads to form $H$ matrices each of size $\tfrac{d}{H} \times d$, where $d$ is the embedding dimension and $H$ is the number of heads. However, we observed higher losses throughout training when using this design.

Still, we believe that there are other settings like GLM-5 where this strategy works well. Such cases would benefit immensely from Gram Newton-Schulz, since the aspect ratio of these weight matrices would be the number of heads $H$. For a standard attention weight like $\mathbf W_q$ with $H=16$ and $T=5$, Gram Newton-Schulz on the little matrices would use $80\times$ fewer FLOPs than orthogonalizing the big matrix!

Model Quality is Preserved

We see loss preserved as follows, when both using the Polar Express coefficients and the coefficients derived by You Jiacheng:¹⁹ Figure 17: Validation perplexity is always preserved within 0.01. We train with Muon using the Chinchilla scaling law on Hopper. Figure 18: Validation perplexity is preserved within 0.01. We train with Muon using the Chinchilla scaling law on Blackwell.

Our Method Speeds up the Optimizer Step

Newton-Schulz Performance We observe that our method speeds up the runtime of the Newton-Schulz step in each iteration by up to $2\times$, especially as weights become more rectangular. The tables below report these speed-ups for each model, benchmarked on both H100 and B300. In these experiments, we use standard Newton-Schulz as the fallback when $m = n$:

Figure 19: Hopper architecture Newton-Schulz time per model weight. Very rectangular weights like Up/Gate and Down in Gemma-1B will especially benefit from Gram Newton-Schulz, while square weights like Llama-430m’s attention weights will just benefit from the kernels. The speedup on MoE-1B for Up/Gate and Down doesn’t even take advantage of the symmetric kernel, since the small intermediate size of $256$ is exactly the tile size. The speedup is fully algorithmic.

Figure 20: Blackwell architecture Newton-Schulz time per model weight. The speedup on MoE-1B for Up/Gate and Down is fully algorithmic, like in Figure 17.

End-to-End Optimizer Performance The following figure shows the end-to-end wall clock time of the optimizer step for each method. For Muon, these timings include the AdamW updates for weights not assigned to Muon (such as the embedding layer and the vector-valued weights), PyTorch operations for splitting and reconcatenating weights, and learning rate scaling.

Figure 21: Hopper architecture end-to-end optimizer step during training, including matrix splitting and recombination for QKV and MLP, LR scaling, master weight updates, and the scalar optimizer (AdamW) step for non-2D weights.

These results allow us to measure the impact of our optimized kernels separately from that of our Gram Newton-Schulz algorithm. We see that both pieces contribute significantly to the speedup. We observe that Llama-430M’s and Qwen-600M’s smaller, square weights benefit from the kernels - again, we stress that square architectures are the rare case. Meanwhile, Gemma benefits from both the algorithm and kernels, seeing the biggest speedup due to its MLP weights’ higher aspect ratio of $8$ instead of $4$.

We run our experiments on a single GPU. The speedup of using our method in different parallelism configurations should be the same as on one GPU in most cases.

Gram Newton-Schulz time in Kimi K2

Kimi K2 is a trillion parameter sparse, fine-grained MoE model with $384$ experts per layer, a hidden size of $7168$, and a small expert intermediate dimension of $2048$. Since models are trending towards finer-grained MoE architectures and Kimi K2 was trained with Muon, this is a perfect setting to benchmark Gram Newton-Schulz.

In the Appendix, we approximate the exposed Newton-Schulz wall clock time of a global training step of Kimi K2 to be that of:

• 216 expert up/gate/down weights of shape $2048 \times 7168$
• 1 dense up/gate/down weight of shape $7168\times18432$

Figure 22: On Hopper, Gram Newton-Schulz is $2\times$ faster than standard Newton-Schulz in Kimi K2’s pipeline parallelism configuration.

Figure 23: On Blackwell, Gram Newton-Schulz is $2\times$ faster than standard Newton-Schulz in Kimi K2’s pipeline parallelism configuration.

Observe that the speedup of Gram Newton-Schulz over standard Newton-Schulz in torch is twice the speedup of standard Newton-Schulz in CuTeDSL over standard Newton-Schulz in torch, showing the contribution of the new algorithm.

Impact on End-to-End Training Time

In the previous section, we showed that Gram Newton-Schulz significantly speeds up the optimizer step time. This improvement is most impactful when the optimizer time is a large share of the global training step time. Many factors affect the relative runtimes of the optimizer step and the forward and backward passes. In this section, we describe several common settings where the optimizer step is a meaningful performance bottleneck.

Low precision training

In low precision training, the forward and backward passes are computed in 4 bit or 8 bit precision, greatly speeding up their wall clock time. However, Newton-Schulz must be computed in 16 bit precision for stability and accuracy. Therefore, the optimizer time will occupy a greater share of training time.

Small global batch size

When global batch size decreases, fewer microbatches are needed, so fewer forward and backward passes will occur per global training step. The optimizer time will remain the same, since it is agnostic to batch size. Therefore, the optimizer step will occupy a greater share of training time. For example, when SFT and RL use Muon, as in Kimi K2’s post-training pipeline, batch sizes are significantly smaller than in pretraining.¹²⁶

Optimizer step frequency is bottlenecked by optimizer duration

Fixing the total number of tokens used in training, smaller global batch sizes are typically preferable to larger global batch sizes for model quality, since they allow for more frequent weight updates.²⁷ However, when using pipeline parallelism at scale, smaller batch sizes can come with a performance tradeoff. The backward pass of pipeline stage $i-1$ needs to hide the optimizer step of pipeline stage $i$ as much as possible, and increasing the batch size to better hide the optimizer step with a longer backward pass can increase throughput.

Gram Newton-Schulz decreases the optimizer step time, allowing the backward pass to hide the optimizer at smaller batch sizes. Thus, Gram Newton-Schulz can improve model quality by allowing for smaller batch sizes and more frequent updates without a throughput tradeoff.

Large cluster size

A larger cluster size allows for more data parallel groups, decreasing the forward and backward pass time of a global training step. The optimizer step time will usually be the same. Distributing the Newton-Schulz work of a GPU’s model parameters across its corresponding rank in the other data parallel groups is possible, but it invokes significant internode communication overhead and occupies bandwidth that is usually not worth the cost.

Conclusion

We hope our analysis and experiments will encourage researchers to try Gram Newton-Schulz. Our results show that Gram Newton-Schulz preserves training quality and speeds up the optimizer step by up to $2\times$ on popular model architectures, providing a rare case of free lunch performance.

We release an implementation of Gram Newton-Schulz that serves as a drop-in replacement for the standard five-step Newton-Schulz used in Muon along with the symmetric GEMM kernels that accelerate it. We believe that the stability analysis provided in this blog post lays the foundation for easily adapting Gram Newton-Schulz to other use cases. The only hyperparameter that needs to be retuned at all is the set of iterations at which to restart. To this end, we provide an autotuning script that takes a series of coefficients (for instance, 10 steps of Polar Express) and suggests the optimal set of restarts according to our analysis above.

Citing this blog post

@misc{GramNewtonSchulz,
  title   = {Gram Newton-Schulz},
  author  = {Jack Zhang and Noah Amsel and Berlin Chen and Tri Dao},
  year    = {2026},
  url     = {https://dao-ailab.github.io/blog/2026/gram-newton-schulz/}
}

References

1. Keller Jordan, Yuchen Jin, Vlado Boza, Jiacheng You, Franz Cesista, Laker Newhouse, and Jeremy Bernstein. “Muon: An optimizer for hidden layers in neural networks.” Blog post, 2024. Available at: https://kellerjordan.github.io/posts/muon/
2. Jeremy Bernstein. “Deriving Muon.” Blog post, 2025. Available at: https://jeremybernste.in/writing/deriving-muon
3. Less Wright and Adnan Hoque. “CUTLASS Ping-Pong GEMM Kernel.” PyTorch Blog, November 1, 2024. Available at: https://pytorch.org/blog/cutlass-ping-pong-gemm-kernel/
4. Noah Amsel, David Persson, Christopher Musco, and Robert M. Gower. “The Polar Express: Optimal Matrix Sign Methods and Their Application to the Muon Algorithm.” International Conference on Learning Representations (ICLR), 2026.
5. Ekaterina Grishina, Matvey Smirnov, and Maxim Rakhuba. “Accelerating Newton-Schulz Iteration for Orthogonalization via Chebyshev-type Polynomials.” arXiv preprint arXiv:2506.10935 (2025).
6. Kwangjun Ahn, Byron Xu, Natalie Abreu, Ying Fan, Gagik Magakyan, Pratyusha Sharma, Zheng Zhan, and John Langford. “Dion: Distributed Orthonormalized Updates.” arXiv preprint arXiv:2504.05295 (2025).
7. Jingyuan Liu et al. “Muon is Scalable for LLM Training.” arXiv preprint arXiv:2502.16982 (2025).
8. Kimi Team. “Kimi K2: Open Agentic Intelligence.” arXiv preprint arXiv:2507.20534 (2026).
9. Aaron Grattafiori et al. “The Llama 3 Herd of Models.” arXiv preprint arXiv:2407.21783 (2024).
10. GLM-5 Team et al. “GLM-5: From Vibe Coding to Agentic Engineering.” arXiv preprint arXiv:2602.15763 (2026).
11. An Yang et al. “Qwen3 Technical Report.” arXiv preprint arXiv:2505.09388 (2025).
12. OpenAI et al. “gpt-oss-120b & gpt-oss-20b Model Card.” arXiv preprint arXiv:2508.10925 (2025).
13. DeepSeek-AI et al. “DeepSeek-V3 Technical Report.” arXiv preprint arXiv:2412.19437 (2025).
14. Han Zhong, Zikang Shan, Guhao Feng, Wei Xiong, Xinle Cheng, Li Zhao, Di He, Jiang Bian, and Liwei Wang. “DPO Meets PPO: Reinforced Token Optimization for RLHF.” arXiv preprint arXiv:2404.18922 (2025).
15. Thomas Pethick, Wanyun Xie, Kimon Antonakopoulos, Zhenyu Zhu, Antonio Silveti-Falls, and Volkan Cevher. “Training Deep Learning Models with Norm-Constrained LMOs.” arXiv preprint arXiv:2502.07529 (2025).
16. Nikhil Vyas, Depen Morwani, Rosie Zhao, Mujin Kwun, Itai Shapira, David Brandfonbrener, Lucas Janson, and Sham Kakade. “SOAP: Improving and Stabilizing Shampoo using Adam.” arXiv preprint arXiv:2409.11321 (2025).
17. Kevin Frans, Sergey Levine, and Pieter Abbeel. “A Stable Whitening Optimizer for Efficient Neural Network Training.” arXiv preprint arXiv:2506.07254 (2025).
18. Vineet Gupta, Tomer Koren, and Yoram Singer. “Shampoo: Preconditioned Stochastic Tensor Optimization.” International Conference on Machine Learning. PMLR, 2018.
19. Gemma Team et al. “Gemma 3 Technical Report.” arXiv preprint arXiv:2503.19786 (2025).
20. Laker Newhouse, Dakota Goldberg, and Ricardo Ruiz. “Faster Symmetric Matrix Multiplication with ThunderKittens.”Available at: https://www.lakernewhouse.com/assets/writing/faster-symmul-with-thunderkittens.pdf
21. Tianyang Lin. “Flash-Muon: An Efficient Implementation of Muon Optimizer.” GitHub repository, 2025. Available at: https://github.com/nil0x9/flash-muon
22. Will Merrill. “Critical Batch Size Revisited: A Simple Empirical Approach to Large-Batch Language Model Training.” arXiv preprint arXiv:2505.23971 (2025). Available at: https://allenai.org/blog/critical-batch-size

Appendix

The share of end-to-end training time taken up by Newton-Schulz can vary widely depending on the training setup. To explain this variability, we analyze two idealized scenarios. In one, standard Newton-Schulz takes 2% of training time; in the another it takes 17%.

Case Study 1: Standard Newton-Schulz accounts for 2% of Kimi K2 training time

The following analysis gives a very optimistic estimate of the optimizer’s wall clock time. We assume an efficient training infrastructure with highly optimized pipeline parallelism. Moreoveer, we assume that the optimizer step of each pipeline stage is completely hidden behind the backward pass of the next pipeline stage.

Kimi K2 Thinking is a $1.1$ trillion parameter model with $32$ billion active parameters. It has $1$ dense layer followed by $60$ MoE layers.¹ It is pretrained with $256$-GPU model parallel groups, $16$-way pipeline parallelism, $16$-way expert parallelism within each pipeline stage, and a huge batch size of $67$ million tokens.

We use a single H100 to approximate the share of each training step’s runtime occupied by Newton-Schulz in this setting under the following assumptions:

1. The training cluster is $2048$ H100s across $256$ nodes (8 GPUs per node), connected with NDR 400 Gb/s InfiniBand inter-node (8 NICs per node, 1:1 NIC-to-GPU ratio) and NVLink 4.0 intra-node. This is the size of the cluster used to train DeepSeekV3, with upgraded hardware.²⁸ This means there are $\frac{2048}{256} = 8$ groups in data parallel.
2. Training in bfloat16 hits $35\%$ to $45\%$ MFU, which is a typical range for MoEs at this scale on H100 clusters.
3. The only non-overlapped optimizer wall clock time is of the last pipeline stage that completes its backward (i.e. pipeline stage $1$ of $16$). The optimizer steps of pipeline stages $2$ to $16$ are fully hidden behind the backwards of stages $1$ to $15$.
4. Pipeline stage $1$ has the dense layer and $3$ MoE layers.

Under these assumptions, the optimal way to partition the Newton-Schulz work of pipeline stage 1 is as follows:

1. Each of the $16$ GPUs in pipeline stage $1$’s expert parallel group gets \(\frac{384 \text{ experts/layer} \times 3 \text{ MoE layers}}{16 \text{ GPUs}} = 72 \text{ experts/GPU} = 216 \text{ expert up-gate-down/GPU}\) Each of the 16 GPUs has its own unique expert weights, so no communication is needed.
2. The four shared experts’ weights and the dense MLP’s weights are divided evenly based on orthogonalization wall clock time amongst the 16 expert parallel GPUs, which run Newton-Schulz in parallel. The dense MLP’s three $7168\times18432$ weights (up/gate/down) dominate the wall clock time, so they are sent to 3 different GPUs, with the rest of the weights split amongst the remaining 13. Thus, the total Newton-Schulz time for all these weights when the 16 GPUs run in parallel is the same as the time to run Newton-Schulz on one of the dense up/gate/down weights. An all_gather is required between the two nodes to collect the distributed orthogonalized gradients, but we assume it is substantially faster than redundant Newton-Schulz work.

Then, the total Newton-Schulz time of Pipeline Stage 1 is that of 216 expert up/gate/down weights and 1 dense up/gate/down weight.

Per our assumptions, Pipeline Stage 1’s Newton-Schulz time is the only non-overlapped Newton-Schulz time. As benchmarked here, standard Newton-Schulz in torch will take 315 ms.

Let’s estimate the end-to-end wall clock time of an entire Kimi K2 global training step.

Given:

• Active parameters: $N = 32 \times 10^9$
• H100 peak: $P = 989 \times 10^{12}$ FLOP/s
• Cluster size: $G = 2048$ GPUs
• Global batch size: $B = 67 \times 10^6$ tokens

For realistic estimates of MFU, we have

Thus, Newton-Schulz takes approximately $\frac{315\text{ ms}}{18140\text{ ms} + 315\text{ ms}} = 1.7\%$ to $\frac{315\text{ ms}}{7060\text{ ms}+315\text{ ms}} = 2.2\%$ of total pretraining wall clock time in this setting.

Case Study 2: Standard Newton-Schulz occupies 17% of Llama3-70B SFT time

Llama3-70B is a 80-layer dense model with hidden size 8192, intermediate size 28672, and grouped query attention with $1024 \times 8192$ $\mathbf W_k, \mathbf W_v$ weights and $8192 \times 8192$ $\mathbf W_q, \mathbf W_o$ weights.²³ Supervised finetuning (SFT) typically uses small batch sizes, ranging from $32$ to $256$ sequences.²⁶²⁸

We construct the following SFT case:

1. Training uses $32$ H100s across $4$ nodes (8 GPUs per node).
2. Training in bfloat16 hits $40\%$ MFU.
3. Weights are sharded evenly across GPUs using FSDP, and the exposed Newton-Schulz time is that of $\frac{80 \text{ layers}}{32 \text{ GPUs}} \approx 3 \text{ layers}$. Each layer has 3 up-gate-down weights, 2 $\mathbf W_q, \mathbf W_o$ weights, and 2 $\mathbf W_k, \mathbf W_v$ weights.

According to our benchmarking, standard Newton-Schulz of

• Nine $8192 \times 28672$ weights takes 738.731 ms
• Six $8192 \times 8192$ weights takes 156.368 ms
• Six $1024 \times 8192$ weights takes 2.318 ms

totalling 250 ms.

Given:

• Parameters: $N = 70 \times 10^9$
• H100 peak: $P = 989 \times 10^{12}$ FLOP/s
• Cluster size: $G = 32$ GPUs
• Global batch size: $B = 64 \text{ sequences} \times 2048 \text{ tokens/sequence} = 131{,}072$ tokens

Newton-Schulz takes approximately $\frac{897.417\text{ ms}}{4350\text{ ms} + 897.417\text{ ms}} = 17\%$ of total SFT wall clock time in this parallelism setting.

[Paper] [Code]

1. Part I
2. Part II

Since the release of Mamba-2 in mid-2024, most architectures have switched from Mamba-1. Why? Mamba-2 made the bet that training efficiency was the largest bottleneck for state space models (SSMs), and thus simplified the underlying SSM mechanism to deliver $2-8\times$ faster training compared to its predecessor, leading to wider adoption.

Since then, the LLM landscape has started to shift. While pretraining is still super important, more attention has been focused on post-training and deployment, both of which are extremely inference-heavy. The scaling of post-training methods, especially with reinforcement learning with verifiable rewards (RLVR) for coding or math, requires huge amounts of generated rollouts, and most recently, agentic workflows, such as Codex, Claude Code, or even OpenClaw, have pushed inference demand through the roof.

Despite the clear, growing importance of inference, many linear architectures (including Mamba-2) were developed from a training-first perspective. To accelerate pretraining, the underlying SSM was progressively simplified (e.g., the diagonal transition was reduced to a scalar times identity). While this brought training speed, it left the inference step “too simple” and squarely memory-bound — the GPUs aren’t brr-ing but moving memory most of the time.

In this new age of inference, we care a lot about pushing the boundaries of the quality-efficiency frontier: we want the better models to run faster.

A natural question arises:

What would an SSM designed with inference in mind look like?

The Mamba-3 Model

What’s missing? The main appeal of linear models is in their name: compute scales linearly with sequence length because of a fixed-size state. Unfortunately, there is no free lunch. The same fixed state size that enables efficient computation forces the model to compress all past information into one representation, the exact opposite of a Transformer, which stores all past information through a continuously growing state (the KV cache) — a fundamental difference. So, if we can’t grow the state, how do we make that fixed state do more work?

We see that earlier designs simplified the recurrence and the transition matrix to make training fast. However, the change also reduced the richness of the dynamics and left decoding memory-bound: each token update performs very little computation relative to memory movement. This provides us with three levers we can pull: (1) make the recurrence itself more expressive, (2) use a richer transition matrix, and (3) add more parallel (and almost free) work inside each update.

From these insights, we improve upon Mamba-2 in three core ways that:

1. increase the expressivity of the SSM mechanism through a more general recurrence derived from our exponential-trapezoidal discretization scheme,
2. expand the state-tracking capabilities by modeling a complex-valued SSM system, and
3. improve the model’s general performance with little impact on decode latency by using multi-input, multi-output (MIMO) SSMs, which model multiple SSMs in parallel, instead of the current single-input, single-output (SISO) SSMs.

Through these three changes, Mamba-3 pushes the frontier of performance while maintaining similar inference latency.

Notably, all three of these changes are inspired by the more “classical” control theory and state space model literature.

Our work goes against the grain of many modern linear architectures, which use alternative interpretations of recurrence (such as linear attention or test-time training) that don’t easily capture these concepts.

Architecture

What has changed in the Mamba-2 layer? Beyond the three methodological upgrades to the core SSM discussed above, we’ve revamped the architecture a bit to make it more in line with conventional modern language models.

Based on the diagram, you’ll notice we’ve changed a couple of things. On a high level,

Norms. We added in QKNormor "BCNorm" in SSM terminology, which empirically stabilizes the training of Mamba-3 models. The addition of this norm brings Mamba-3 in line with contemporary Transformer and Gated DeltaNet (GDN) models. With QKNorm, the RMSNorm from Mamba-2 becomes optional. However, we empirically find that it may still be worth keeping in hybrid models due to helping length extrapolation capabilities. More on this later.

Goodbye Short Conv. We’ve been able to get rid of the pesky short causal convolution of Mamba-1/2 by combining (1) simple biases on B and C after BCNorm with (2) our new discretization-based recurrence. The new recurrence implicitly applies a convolution on the input to the hidden state, and we show how this is the case in Part 2 of our blog.

Finally, you’ll notice a couple of new components, namely RoPE and MIMO projections. The RoPE module expresses complex-valued SSMs via the interpretation of complex transitions as rotations, forgoing the costly reimplementation of kernels. The MIMO projections expand the B and C matrices to the appropriate representation needed for MIMO SSMs.

We dig into the motivation and exact implementation of these two in greater detail in the second part of our blog (lots of goodies there 🎁), so for now, just think of them as standalone, fundamental improvements that individually contribute to improving the model’s performance and/or capabilities.

Finally, our overall architecture now adopts interleaved MLP layers following the standard convention of Transformers and other linear models.

Empirical Results

We evaluate our final Mamba-3 model against other popular linear alternatives and the Transformer baseline.

Language Modeling

We find that our new Mamba-3 model outperforms the prior Mamba-2 model and strong linear attention alternatives, such as GDN, on language modeling across various pretrained model scales. Mamba-3-SISO is directly comparable to prior linear models; for example, it matches Mamba-2 exactly in architecture shapes (model dimensions, state size, etc.) and has comparable training time. Our MIMO variant of Mamba-3 further boosts accuracy on our downstream tasks by more than 1 percentage point over the regular Mamba-3 at the 1B scale, with the caveat that MIMO requires longer training times but not longer decoding latencies!

Retrieval Tasks

Linear models, with their fixed-size state, naturally underperform their Transformer counterparts on retrieval-based tasks. As expected, within pure models, the Transformer is superior on retrieval tasks, but Mamba-3 performs well within the class of sub-quadratic alternatives. Interestingly, the addition of MIMO further improves retrieval performance without increasing the state size.

Given this innate deficit but overall strong modeling performance,

we predict that linear layers will be predominantly used in conjunction with global self-attention layers in the future. $^*$

$^*$ at least for language modeling

Hybrid models that combine the general memory-like nature of linear layers with the exact database-like storage of self-attention’s KV cache have been shown empirically to outperform pure models while enabling significant memory and compute savings , and we do find here that the combination of linear layers with self-attention enables better retrieval compared to a vanilla Transformer.

However, we highlight that the exact way that these linear models interact with self-attention is not fully understood. For instance, we find that the use of the optional pre-output projection for Mamba-3 improves the length generalization performance on the synthetic NIAH tasks at the slight cost of in-context real-world retrieval tasks. Furthermore, even the details of the returned norm such as placement, e.g., pre-gate vs post-gate, and type, grouped vs regular, have non-negligible effects on accuracy on tasks composed of semi-structured and unstructured data, such as FDA and SWDE.

Kernels Here, There, and Everywhere

We’re excited to see what people build with Mamba-3. To help facilitate this, we are open-sourcing our kernels, which are on par in terms of speed with the original Mamba-2 Triton kernels.

Benchmarking Latencies

Prefill Latency

Prefill+Decode Latency

When comparing models at the 1.5B scale, Mamba-3 (SISO variant) achieves the fastest prefill + decode latency across all sequence lengths, outperforming Mamba-2, Gated DeltaNet, and even the Transformer with its highly optimized vLLM ecosystem. Furthermore, Mamba-3 MIMO is comparable to Mamba-2 in terms of speed but has much stronger performance.

Mamba-3 SISO’s Triton-based prefill maintains nearly identical performance to Mamba-2, demonstrating that the new discretization and data-dependent RoPE embeddings do not introduce additional overhead, while Mamba-3 MIMO only incurs a moderate slowdown for prefill due to its efficient TileLang implementation. The strong decode performance for both Mamba-3 variants can be partially attributed to the CuTe DSL implementation, which was made significantly easier by the simplicity of Mamba-3 components.

Design Choices

We spent a lot of time thinking about how to make the kernels as fast as possible without compromising on ease-of-use. We ended up using the following stack: Triton, TileLang, and CuTe DSL.

The use of Triton was quite an easy choice. It’s pretty much standard for architecture development (the great flash linear attention repo is purely in PyTorch and Triton) for good reason, as it enables better performance than standard PyTorch by enabling controlled tiling and kernel fusion while being a platform-agnostic language. Triton also has some pretty nifty features, like PTX (a GPU-oriented assembly language) injection and its Tensor Memory Accelerator support (on Hopper GPUs) for bulk, asynchronous transfers from global to shared memory.

Our MIMO prefill kernels were developed with TileLang instead. The additional projections corresponding with the variant present an opportunity where we can reduce memory IO via strategic manipulation across a GPU’s memory hierarchy. Unfortunately, Triton didn’t provide the granularity of memory control we desired, so we opted for TileLang, which allows us to explicitly declare and control shared-memory tiles and create register fragments, reusing memory more efficiently while still being high-level enough for us to develop the kernels quickly.

Since we’ve been hammering the importance of inference and decode, we decided to use CuTe DSL for our decode kernels. Through its Python interface, we’re able to generate low-level kernels using high-level abstractions from CUTLASS. Here, we practically have CUDA-level control, enabling us to develop highly-performant kernels tailored to the specifications of our hardware (Hopper GPUs, in this case). With fine-grained control over tensor layouts and warp specialization, we built a kernel that takes advantage of all the bells and whistles in the GPU.

Importantly, these implementations across varying levels of GPU abstraction are made possible by the underlying algorithmic design of Mamba-3’s simple, lightweight additions and their clever instantiations. We discuss details such as the exact fusion structure and kernel DSL in more depth in our full release.

Next Up

Glad you made it to the end of Part 1! There were a lot of details regarding our kernels and experimental results and ablations we didn’t have time to cover in this post, but don’t fret! Everything can be found in our paper, and the kernels have been open-sourced at mamba-ssm!

Up next, the second (and final) part of the series delves into the three core improvements to Mamba-3 and their SSM foundations, and gives some directions we’re especially interested in.

1. Part I
2. Part II

We introduced our Mamba-3 model in Part I in which we mentioned that the three core methodological changes were inspired by the SSM perspective. Here, we’ll actually do a deep dive into what each of these three improvements entail, their motivations, and their derivations.

But first, let’s refresh our memory on the underlying state space model and its background.

State Space Foundations

The state space model, at its most primitive, is a simple, continuous ordinary differential equation (ODE). The input $x(t) \in \mathbb{R}$ is mapped to output $y(t) \in \mathbb{R}$ through a hidden state $h(t) \in \mathbb{R}^N$ of size $N$, also referred to as the state size. In the past, in both deep learning and classical control theory, these systems were linear time-invariant (LTI), where the “state decay” transition $A \in \mathbb{R}^{(N\times N)}$, $B \in \mathbb{R}^{N}$, and $C \in \mathbb{R}^{N}$ terms were constant.

We will occasionally refer to $A$ as the state-transition, and $Bx(t)$ as the state-input.

Upon discretization with one’s favorite method, as demonstrated with the zero-order hold (ZOH) used in both Mamba-1 and Mamba-2, a familiar recurrence materializes,

where the discretized $\bar{A}$ and $\bar{B}$ are now $e^{\Delta_t A_t}$ and $A_t^{-1}(e^{\Delta_t A_t} - I)\,B_t$ respectively.

Eagle-eyed readers may ask “how does one go from a LTI system to a linear-time varying (LTV) system?” — if you did, the answer is revealed below!

While there are no theoretical restrictions on the class of matrices $\bar{A}$ can be, computational constraints keep transition matrices structured, e.g., diagonal, scalar times identity, Householder (identity plus low-rank), etc.

Great, now we’ve set up the underlying mechanism of Mamba used in both Mamba-1 and Mamba-2!

As a quick recap, Mamba-3 builds on Mamba-2 to improve the efficiency-performance trade-off of current SSMs with inference at the forefront. The three core improvements we’ve been discussing in this post are rooted in classical state space theory:

1. Instantiating a more generalized recurrence through a formal framework for discretizing the underlying ODE
2. Improving state-tracking abilities by converting to complex-valued SSM without the engineering challenges of explicit complex numbers
3. Increasing the expressivity of the SSM without increasing state size through a multi-input, multi-output (MIMO) formulation.

Let’s jump straight into it.

Upgraded Discretization

Our end goal is to obtain a more general recurrence than that of current models from first principles. Luckily for us, the discretization of the continuous ODE provides the perfect opportunity to do so.

But first, let’s lay down the foundation for our framework used in discretizing time-varying systems. Remember how we mentioned that prior Mamba discretizations adapted the canonical ZOH discretization by adding a time subscript to convert the method from LTI to LTV? Well, to be honest, we left a bit more out earlier. The actual implementation of Mamba frankensteined the canonical ZOH and Euler methods to create discretized parameters $\bar{A}_t = \exp(\Delta_t A_t), \bar{B}_t=\Delta_t B_t$.

Holy heuristic! But it works empirically ¯\(ツ)/¯.

One potential explanation for why this mixture does so well despite not being theoretically grounded is that Euler is an approximation of ZOH. Taking the ZOH formula for discretized $\bar{B}_t=A_t^{-1}\left(\exp(\Delta_t A_t) - I \right) B_t$, if we use the approximation $\exp(x) \approx 1+x$, the resulting $\bar{B}_t \approx \Delta_t B_t$.

This heuristic was always bugging us in the back of our minds, so in our work, we finally formalized the discretization.

We develop a method that produces a class of formal discretizations for time-varying systems, including one called exponential-Euler that exactly corresponds to the formula used in Mamba-1/2.

Exponential-Adjusted Discretizations

So let’s actually figure out how to discretize our LTV system in a principled manner.

The general intuition behind our framework is that a bare-bones ODE $f'(t) = Af(t)$ has a closed-form solution $f(t) = e^{tA} f(0)$. It follows that the one-step discrete update is then $x_{t+1} = e^{\Delta A}x_t$. Here, since the derivative includes $Ah(t)$, the state directly impacts the rate of change. Thus, the parameterization of A can rapidly oscillate the dynamics of the system, which forces explicit methods, like Euler, to take small $\Delta$ steps which limits the expressivity of the system.

To mitigate this, we adjust the dynamics with an integrating factor of $e^{-At}$ to counteract the dominating exponential and directly analyze $e^{-At}h(t)$ instead. Let’s see how it applies to our system.

Taking our $h'(t)=A(t)h(t)+B(t)x(t)$ system, we apply an integrating factor of $e^{\int_0^t -A(s)ds}$ as $A$ is now time-varying.

since $(e^{\int_0^t -A(s)ds})' = -A(t)e^{\int_0^t -A(s)ds}$.

Thus, when we want to discretize between timesteps $[\tau_{t-1}, \tau_t]$, we can just integrate both sides over that interval. For ease of notation, we denote $z(t) := e^{\int_0^t -A(s)ds}$.

Rearranging into a more familiar form and substituting back the $z(\tau)$ value:

Now, we’ve isolated the state-transition and the state-input through our integration factor. This means the most “difficult” part of the adjusted system can be calculated independently of the state-input integral, which is left to be approximated with many possible methods.

Under the LTV case, because $A(s)$ is continuous, we “sample” it with a right-hold assumption where $\forall s \in [\tau_{t-1},\tau_t], A(s) = A(\tau_t) = A_t$, resulting in

This final equation lays the foundation for recovering the prior Mamba discretization methods and is also the inspiration of our “exponential-“ style name, as the application of the integration factor can be seen as a style of exponential tilting or adjustment.

Recovering Prior Mamba Discretization

As previously mentioned, prior Mamba discretizations differ on paper and in practice. Now, using our new discretization derivation and certain sampling assumptions, we can recover the reported LTV ZOH discretization and the implemented exponential-adjusted Euler discretization scheme, or exponential-Euler for short.

We have already recovered the $\bar{A}$ term for both, so we will focus only on the remaining state-input integral which evaluates to $\bar{B}$.

ZOH: Assuming similar assumptions where $B(\tau), x(\tau)$ are constant and sampled at the right endpoint,

Exponential-Euler: Once again, we approximate the integral with Euler’s rule and hold the $B, x$ terms to the right endpoint.

New Exponential-Trapezoidal Discretization

Thus, the linchpin of converting continuous-time SSMs into various tangible recurrences is approximating $\int_{\tau_{t-1}}^{\tau_t} \exp\left((\tau_t - \tau)A_t\right)B(\tau)x(\tau)d\tau$ in different ways. We’ve shown above that one can either analytically solve it (ZOH) or approximate it (Euler), but what if we don’t want to use inverses but also want something more precise than Euler’s?

We can instead use the trapezoid method to approximate the integral using both endpoints instead of just one for Euler. Unlike the standard method which averages both endpoints, we use a convex combination which we find empirically performs better. The integral then evaluates to

Interestingly, we can see here that for our new exponential-trapezoidal recurrence, there is some structured time-mixing across the state-input terms. Thus, it acts as an implicit data-dependent convolution of size two on the SSM’s state-input.

Parallel Representation of New Recurrence

Now how can we format our recurrence in a parallel representation to enable faster training? To do so, we’ll be viewing the recurrence in its parallel form. This hearkens back to the state space duality (SSD) framework introduced in Mamba-2.

Let’s rewrite our recurrence so this doesn’t get too messy:

where $\alpha_t = e^{\Delta_t A_t}, \beta_t=(1-\lambda_t)\Delta_t e^{\Delta_t A_t},\gamma_t=\lambda_t\Delta_t$.

If we expand the recurrence where $h_{-1}=0$,

, we can express the output as a matrix operation

which can further be decomposed into a 1-semiseparable matrix (Mamba-2’s decay mask) and a 2-band matrix.

The equivalence established between the recurrent and parallel forms of Mamba-3 is another instance of what Mamba-2’s SSD established: that certain classes of SSMs have a matrix form that vectorizes the recurrence. This forms the foundation of the hardware-efficient algorithm used for training.

Complex-valued SSM

As we’ve mentioned, the simplification of the SSM over the past couple years to improve efficiency has reduced the abilities of newer modelsWe've mainly been highlighting the simplification of diagonal to identity times scalar across the LTV systems of Mamba-1 to Mamba-2, but the original LTI SSMs were actually complex-valued! Mamba-1 simplified the SSM to be all real-valued which empirically did not impact language modeling, but as we will see, reduced state-tracking capabilities. . This has been corroborated by a whole host of work which finds that linear RNN-style models are theoretically constrained on state-tracking tasks by their lack of non-linearity between timesteps and their structured matrix transitions, both of which, unfortunately, are critical to their efficient computation .

While more complex state transitions, such as diagonal plus low-rank (DPLR) in older LTI SSM models, can improve the method’s expressivity, the simplification of transitions across iterations of LTV SSMs has resulted in even the simplest state-tracking tasks falling out-of-reach for Mamba-style models Related delta-rule based linear attention models, e.g., GDN, KDA, are able to partially mitigate these state-tracking limitations through more expressive state transitions, i.e., identity plus low-rank. . The inability to solve some of these state-tracking synthetics may signal poor performance in practice where models might need to keep track of parentheses and diffs for coding or actions and states throughout a story.

Parity, what is that?

One of the simplest tasks, parity, determining whether the sum of a sequence of 0’s and 1’s is even, is unsolvable by Mamba models in a constant number of layers. The ideal solution requires the hidden state to track whether the running sum is even or odd and to alternate depending on the next input, modeling a simple two-state automaton . While this seems simple enough, current Mamba models constrain the transition $\bar{A}_t \in [0,1]$, which forces the model to learn the naive solution: add all the values together then mod 2 If $\bar{A}_t$ can be -1, it would enable the alternating solution, but would require the underlying implementation to be rewritten as currently the $\bar{A}$ is handled in log-space. . This does work for shorter sequences but quickly becomes infeasible when the sequence outgrows the state.

But, parity and other modulo tasks can be solved with rotations! The way one can visualize how rotations solve modulo $m$ problems is that one has some 2D vector that can be rotated around the origin. The entire possible angle distribution $[0, 2\pi]$ is partitioned into $m$ sections, and the vector is rotated by $\tfrac{2\pi}{m}$ to align with the current running modulo remainder.

Representing with Real-valued SSMs

Working with complex values in computer systems is quite a pain due to their multiplicative interactions. Luckily for us, diagonal complex-valued continuous SSMs can be represented as discretized real-valued SSMs (without any additional approximation loss compared to standard discretization).

While the full proof can be found within our paper, the general intuition is to expand the original $N$-sized state complex-valued SSM to a $2N$-sized real-valued where each complex-valued dimension is split into its real and imaginary counterpart, and the complex transition matrix is partitioned into its scaling and oscillatory portions. With the commutative property of the scaling and oscillatory components in effect (due to the diagonal structure of the underlying matrix), we can map the continuous diagonal complex transition into a block-diagonal, scaled rotation transformation.

Eventually, under the prior exponential-Euler discretization, we obtain the following recurrence

for an $N=2$ state. For larger states, the rotation matrix $R_t$ is block-diagonal and the $\theta$’s can differ.

Efficient Implementation with RoPE Trick

Great, now we’ve shown that we can implement a complex SSM without having to explicitly model the imaginary components! But another issue remains: the rotation of the hidden state requires us to reimplement the kernels to incorporate this new type of transition — more moving parts, rotating the entire hidden state, etc., — seems like quite the hassle ugh… or is it?

Luckily for us, given the structure of $A$, we can sidestep all of this and directly adjust the $B, C$ to achieve the same goal. This is because the output for timestep $t$ can be modeled as

Since $\bar{A}$ is a scaled identity matrix, we can ignore the $\bar{A}$ terms for now by absorbing them into $C$. This results in the term $C_i^\top R_i \cdots R_{j+1} \bar{B}_j$ which can be represented by $\left(R_i \cdots R_0 C_i\right)^\top \left(R_j \cdots R_0 \bar{B}_j\right)$. The $\bar{A}$ terms can be reintroduced at this point. Thus, it’s apparent that the rotations can be embedded into the $B, C$ terms prior to performing the SSM recurrence instead of directly adjusting the transition matrix.

The application of our data-dependent rotations onto $B, C$ can be done efficiently. Instead of performing numerous matrix multiplications, we can run a cumulative sum over the $\theta$’s and perform the efficient realization of rotary matrix multiplication from the RoFormer paper , which itself used data-independent rotations. This inspired us to call the use of a vanilla SSM to compute a complex SSM as the “RoPE trick.”

The RoPE trick extends to our exponential-trapezoidal recurrence, and we empirically validate that our complex-valued SSM is able to solve state-tracking tasks previously too hard for prior Mambas.

Multi-Input, Multi-Output

The compute paradigm in scaling LLMs has shifted from training to inference in the past two years or so. Nowadays, more and more compute is dedicated to the actual deployment and usage of these models, and to some degree, the writing was on the wall. Emergent properties such as chain-of-thought and in-context learning techniques dramatically improved performance of earlier models by making them think longer and process more tokens, and all of the best models to date are reasoners which have (almost certainly) been post-trained with reinforcement learning using large rollout budgets. With the advent of agentic workflows, we have agents spawning subagents and so forth.

What does such a paradigm change mean for hardware efficiency?

Working while Memory-Bound

Compared to the compute-bound nature of training, the deployment of the same models, especially decoding, is memory-bound. Throughout training, the hardware is constantly performing operations, but during decoding, the compute units of the hardware sit idle for large swathes of time as it waits for data to be moved across different levels of memory hierarchy.

As an example of why this happens, think about a simple MLP. During training, the entire sequence is processed, but during decode, only the current token is processed as the past tokens are cached. The latency spent moving the MLP weights is around the same for both training and decode, but can be amortized a lot better over more computation under a training regime.

So with current linear models where the state update and output calculation can be performed in constant time, compute units sit idle for most of the time, and we are bottlenecked by simply moving data back and forth! One way to estimate how “hard” the hardware is working is through arithmetic intensity, a ratio of compute performed to memory moved.

Let’s analyze how SSMs are deployed in practice and their arithmetic intensity. A typical SSM, say Mamba-2 for instance, is organized into heads with head dimension $P$, where a single head is composed of $P$ SISO SSMs that share the same $a_t, B_t, C_t, B_t$

where $a_t$ is a scalar decay and $\mathbf{x}_t, \mathbf{y}_t \in \mathbb{R}^{P}, \mathbf{h}_t \in \mathbb{R}^{N\times P}$. If we use 2-byte data, for a single decode step, the total memory traffic is $2(1 + 2N + P + NP)$ when accounting for all SSM parameters. The movement of the hidden state is clearly the main contributing factor at reasonable values of $P$ and $N$.

When calculating the number of FLOPs used for the same operation, we get around $5NP - P$ A quick rundown why. The $a_th_{t-1}$ scaling, $B_tx_t$ outer product, and their summation take a total of 3NP. The matmul between $C_t^\top h_t$ takes $2N - 1$ per $P$ dimension ($N$ multiplication and $N-1$ accumulation), resulting in a final $5NP - P$.. Thus, default SSM decoding has an arithmetic intensity of around $2.5$. To put this into context, the arithmetic intensity of matmuls for an H100 is around $300$ ops per byte; anything above this is compute-bound. Having an arithmetic intensity of as low as $2.5$ means that decoding is squarely memory-bound… yikes

Since we pay for the entire rack and the expensive tensor cores, how can we use as many of them as possible?

The MIMO System

We’ve seen empirically that the state size is quite important for performance but expanding it also increases memory… so, let’s keep that the same. Now how do we increase the compute required for calculating the hidden state recurrence while maintaining the same hidden state? Referring back to our state space/control theory toolbox, multi-input, multi-output (MIMO) SSMs can be used instead of the single-input, single-output (SISO) SSMs we’ve been using.

Through the expansion of the dimension of $\mathcal{C}_t, \mathcal{B}_t$ to $N \times R$ and $\mathbf{x}_t, \mathbf{y}_t$ to $P \times R$ where $R$ is the rank of the system, we can maintain similar memory traffic (for small enough $R$) while increasing the FLOPs utilized when operating with matrix multiplications with $B_t x_t^\top$ instead of outer-products.

The total FLOP count thus increases to $4NPR + NP - PR$ which results in an arithmetic intensity that scales with $O(R)$ when $R \ll P, N$ (generally the case as $P=64, N=128$ and $R=4$).

Intuition and Training

The downstream gains and comparable decoding latency associated with switching from SISO to MIMO require compute costs that scale linearly with $R$ during compute-bound training.

Expressing the output of a MIMO SSM would require $R^2$ SISO SSMs due to its rank $R$ state-input and $R$ unique outputs. Its hidden state can be partitioned into the sum of $R$ SISO hidden states, and subsequently, the hidden state needs to be instantiated $R$ times for each of the outputs. But if the expressivity is a $R^2$ increase, how does training compute required scale by only $R$?

The chunked training algorithm is the reason for this disparity. Most linear models, including both Mamba-2 and Mamba-3, are computed in chunked fashion, where the sequence is partitioned into chunk sizes of $C$. The hidden state is aggregated across chunks in a sequential manner, while the output of the SSM is calculated with a quadratic, parallel algorithm.

For MIMO, the computation of outputs between chunks increases by a factor of $R$, whereas the computation of outputs within each chunk increases by $R^2$. So by decreasing the chunk size to $\tfrac{C}{R}$, the total FLOP count only increases by a factor of $R$. Our paper covers the actual FLOP calculations, but one way to think about it is that we want to reduce the amount of compute required for each quadratic algorithmic pass by increasing the number of times we call it.

Instantiation

Given the interpretation of MIMO SSMs as multiple SISO ones, improvements introduced for vanilla SSMs, like our exponential-trapezoidal discretization and complex-valued transition, can be directly applied to our MIMO variant. However, the conversion must be done carefully without drastically increasing the total parameter count. The naive solution of expanding the projection size would lead to a $R\times$ increase as the SSM inputs $x, B, C$ would all need to be adjusted. The subsequent rank $R$ output $Y$ would also force the output gate $Z$ and output projection to expand as well. This approach is clearly untenable.

Instead, we can use Mamba’s multi-value attention structure to our advantage. Since the $B, C$ are tied across all heads, we can increase the projection size without much issue, resulting in a fairly negligible $DN \to DNR$ increase for the entire layer. However, the input $x$, output $y$, and gate $Z$ are unique per head and are the main source of parameters, thus cannot be increased in such a way. Instead, we keep the original projections then element-wise scale each dimension of the projected value to size $R$ using a learnable, data-independent vector. For each head, we are able to reduce the parameter count from $DPR$ to $DP + PR$, which is quite the reduction given the number of heads each Mamba layer has!

We show that our instantiation balances the expressivity of multi-input, multi-output systems and parameter efficiency. In parameter-matched settings, our Mamba-3 MIMO variant further improves the already strong performance of regular Mamba-3 at all scales we tested on. When analyzing state size (proxy for decoding speed) to performance in controlled experiments, Mamba-3 sets the Pareto front compared to prior Mamba-2, able to achieve comparable performance with half the state size.

Mamba-3 offers a faster model with the same quality or a better model for the same speed.

The End, For Now

We had to cut a bunch of proofs and results to keep the content in here digestible, but if that interests you, please do read our paper!

Within our work, we’ve aimed at boosting the performance and capabilities of the Mamba series from a few SSM-centric improvements. We’re curious to see how and where the community explores in architecture research. In particular, we are quite excited (and think addressing them would be really impactful) in the following directions:

• Building better hybrids: It’s been amazing to see the general research community and industry labs appreciate the benefits linear models can provide, especially with hybrid models . Most architectures follow an interleaved structure, but the “science” of what enables good linear-self attention synergy is still unknown. We’ve seen a lot of cool work making important ground, e.g., shifting from RoPE to NoPE for attention layers or keeping the first and last layers attention-free A more meta question might be: are interleaved hybrid models truly the best way to utilize linear models?

• Improving Layer Primitives: Our methodological improvements, while most natural to SSMs, can be applied to other architectures. It would be interesting to see how they scale under different transition mechanisms. In addition, there seems to be a whole trove of untapped improvements waiting to be uncovered or inspired in the “classics,” if you will. Just as Mamba and other SSMs are grounded within signal processing and traditional state space literature, such parallels can be found in other types of linear models — fast-weight programmers for linear attention , for example. What might the standard transition look like for the best self-attention alternative in two, three years?

Modern accelerators like Blackwell GPUs continue the trend of asymmetric hardware scaling, where tensor core throughput grows far faster than other resources such as shared memory bandwidth, special function units (SFUs) for transcendental operations like exponential, and general-purpose integer and floating-point ALUs. From the Hopper H100 to the Blackwell B200, for instance, BF16 tensor core throughput increases from 1 to 2.25 PFLOPs, while both the SFU count and shared memory bandwidth remains unchanged.

This scaling asymmetry has profound implications for optimizing complex kernels like attention for the Blackwell architecture. At its core, attention comprises two GEMMs ($S = Q \cdot K^T$ and $O = P \cdot V$) with softmax in-between; in practice, it also involves substantial plumbing and bookkeeping: data movement, synchronization, layout transforms, element-wise ops, scheduling, masking, etc.

A naive viewpoint on attention might be that the speed of the GEMMs completely controls the kernel performance and one can effectively disregard these other attention components, at least to first order. However, doing a “feeds and speeds” analysis for B200 in fact shows the opposite: the main performance bottleneck lies not in how fast the tensor cores can do MMA, but rather (a) in the SFU units for softmax exponential during the FWD computation, and (b) in the shared-memory traffic during the BWD computation.

In this blog post, we present FlashAttention-4, an algorithm and kernel co-design that maximizes overlap between matmul and these other resource bottlenecks. On B200 with BF16, it reaches up to 1605 TFLOPs/s (71% utilization), up to 1.3x faster than cuDNN version 9.13 and 2.7x faster than Triton.

Our main algorithmic and kernel co-design ideas are as follows:

1. New pipelining for maximum overlap: New forward and backward software pipelines that exploit Blackwell fully asynchronous MMA and larger tile sizes, overlapping tensor cores, softmax exponential, and memory operations.

2. Forward (FWD) pass: A software emulation of the exponential function implemented via polynomial approximation on FMA units to mitigate the exponential bottleneck, plus conditional online softmax rescaling.

3. Backward (BWD) pass: Storing intermediate results in tensor memory to relieve shared-memory traffic, combined with Blackwell’s new 2-CTA MMA mode to reduce shared memory traffic further and also cut atomic reduction in half, and additional support for deterministic execution mode for reproducible training.

4. Scheduling: New tile scheduler to mitigate load imbalance from causal mask and variable sequence length.

New hardware features on Blackwell

Tensor memory (TMEM): On B200, each of the 148 SMs has 256 KB of TMEM, an on-chip scratchpad wired into the tensor cores for warp-synchronous intermediate storage.

Fully asynchronous 5th gen tensor cores: tcgen05.mma is asynchronous and accumulates in TMEM. For BF16 and FP16, the largest single CTA UMMA tile is 128x256x16, which is about 2x larger than the largest Hopper WGMMA atom. UMMA is launched by a single thread, easing register pressure and making larger tiles and deeper pipelines practical without the spilling pain points of Hopper warpgroup MMA. This also makes warp specialization more viable, with some warps moving tiles while others issue MMA to overlap matrix multiply accumulate with softmax and memory traffic. tcgen05.mma can also source operand A from TMEM.

2-CTA MMA: Blackwell can execute one UMMA across a CTA pair in the same cluster, spanning the TMEM of both peer CTAs. One thread in the leader CTA launches the MMA, but both CTAs must stay active while it is in flight. This scales the MMA tile dimension up to 256x256x16 by splitting M and N across the pair, reducing redundant traffic and lowering per-CTA footprint. The CTA group size, 1 or 2, must remain constant across TMEM and tensor core operations within a kernel.

Feeds and Speeds

For M=N=D=128, here are the feeds on B200 (per SM):

• Tensor Cores (BF16): 8192 ops/cycle
• Exponential unit: 16 ops/cycle
• Shared Memory traffic: 128 bytes/cycle

And the speeds (clock-cycles per tile):

Forward (2 MMAs + MN exp):

• Tensor Cores: 1024
• Exp: 1024
• SMEM: 768

Backward (5 MMAs + MN exp) — 1-CTA:

• Tensor Cores: 2560
• Exp: 1024
• SMEM: 3328

Takeaway: Forward is bottlenecked by compute and exponential, backward is bottlenecked by shared memory bandwidth. So we overlap softmax with MMA in the forward pass and reduce shared memory traffic in the backward pass.

Forward pass: New softmax pipelining with conditional rescaling

The forward pass has two matmuls, QK^T and PV. On Blackwell, tensor cores got much faster, but the exponential unit (MUFU.EX2) did not. So softmax is no longer “just the thing between the two matmuls” — it is a bottleneck that must be carefully pipelined.

The FWD pass in short:

• Ping-pong schedule 2x Q and 2x O tiles per CTA: maximize overlap between MMA and Softmax
• 2x softmax warpgroups: per-tile softmax with synchronization to not overlap when computing exponential
• Software emulation of $2^x$: distribute exp computation across hardware’s MUFU and software emulated on FMA
• Store P in TMEM in stages: mitigate register pressure
• Correction warpgroup: designated “correction” warpgroup to perform rescaling to remove from critical path
• Online softmax (conditional) rescaling: Rescale less frequently to minimize non-matmul operations

Pipeline: Ping-pong Q tiles plus a dedicated correction stage

FlashAttention-4 computes two query tiles per CTA — $Q^H$ and $Q^L$ — each covering 128 query tokens, and alternates them in a ping-pong schedule.

Blackwell changes the softmax mapping. The accumulator tile for S = QK^T is 128x128 and lives in tensor memory; however, upon being read into registers, we have one thread per row for the partitioning of the tile as dictated by the hardware. We use two 128-thread warpgroups, one per Q tile, and each softmax warpgroup executes the following sequence of operations:

1. Each thread loads one 128-element row of S from tensor memory into registers
2. Reduce rowmax and rowsum
3. Using a tunable parameter, decide which portion of the 128 elements uses hardware’s MUFU vs. software-emulated $e^x$
4. Compute P = softmax(S) and convert to BF16 precision
5. Store P back to tensor memory in stages to relieve register pressure (as opposed to holding 128 elements of S and 64 BF16 elements of P simultaneously)
6. Trigger the corresponding PV matmul as soon as a 3/4 chunk of P is stored

The critical detail is that exp is the bottlenecked section. We explicitly synchronize the two softmax warpgroups so they do not evaluate exp at the same time, thereby reducing MUFU contention.

To keep rescaling off the critical path, the kernel assigns it to a dedicated warpgroup. The correction warpgroup computes:

Only rescale when the max jump is large:

Apply the final normalization at the end of the iteration $O_{\text{final}} = \frac{O}{l_{\text{final}}}$.

At the end we still normalize using the true final statistics, so skipping small rescale steps preserves the final output while deleting many vector computations from the critical path. We make the decision at warp granularity to avoid divergence.

Faster exponential: Distribute 2^x across MUFU.EX2 and FMA

Softmax requires many exponentials, and MUFU throughput is much lower than tensor core throughput. FlashAttention-4 increases effective exp throughput by running the software emulation of exp2 alongside the hardware MUFU.EX2 path, using FMA units that would otherwise be underutilized.

Range-reduction (Cody-Waite): We use the classical technique of Cody-Waite range reduction to decompose the exponential computation into the integer and the fractional part: $2^x = 2^{n} \cdot 2^{f}$. In IEEE 754 float32, scaling by $2^n$ is just an exponent update.

Polynomial approximation of $2^{x_\text{frac}}$ (Horner’s Method): To approximate $2^f$ we rewrite in Horner’s form for efficient evaluation.

The coefficients p0 = 1.0, p1 ≈ 0.6951, p2 ≈ 0.2276, p3 ≈ 0.0771 are chosen using the Sollya software package to minimize the relative approximation error over $[0, 1)$.

Exponent bits shift and add: The final step is to combine the integer part $n$ and the fractional approximation $2^f$ to form $2^{x} \approx 2^{n}\cdot 2^{f}$. Since $2^f \in [1,2)$ has float32 exponent 127, multiplying by $2^{n}$ is just shifting the integer $n$ into the exponent field and then adding the mantissa bits of $2^{f}$.

Backward pass: Where shared memory traffic dominates

Optimizing FlashAttention backward can feel like stuffing an oversized rug into a room: flatten one corner and another pops up. Backward computes about 2.5x the tensor core work of the forward pass, chaining five MMA operations to recompute S and run the QK and PV gradient MMAs for dQ, dK, dP, and dV, plus the element-wise work for P and dS. On Blackwell, FLOPs are not the limiter for backward; shared memory bandwidth is.

Pipeline: Overlap MMAs with softmax

Hopper-era FlashAttention-3 keeps MMA accumulators in registers, so register pressure often forces a more serial schedule. On Blackwell, accumulators live in TMEM, which makes it practical to keep multiple MMAs in flight while the CUDA cores handle the element-wise work for P and dS. Since exponential throughput is comparable to two MMAs in our roofline, hiding it is worth it.

The key overlap is simple: while we compute softmax for tile j, we already issue the dK and dQ MMAs for tile j-1.

To reduce shared memory traffic, the backward pass recomputes S and P in a transposed tile relative to the forward pass, so the intermediate is already $S^T$ and $P^T$. We can then store $P^T$ (and later $dS^T$) directly in TMEM in the exact operand A layout consumed by the dV and dK MMAs respectively.

TMEM cannot hold five full accumulators and intermediates at once, so FA4 reuses TMEM columns across stages: S and P share one set of columns, and dP, dS, and dQ share another.

2-CTA backward pass: Reducing shared memory traffic and global atomic adds

Shared memory traffic. Even with the improved pipeline and with two of the ten GEMM operands kept in tensor memory, the backward pass is still limited by shared memory bandwidth. We mitigate this with Blackwell 2-CTA MMA mode, which partitions the output accumulator across the CTA pair. With M=256 and N=K=128, the two CTAs cooperate as one tile: each CTA stages half of operand B and keeps only its own accumulator slice. This roughly halves shared memory traffic for operand B.

Reduction axis conflict. We use M=256 and N=K=128 MMA tile across the five backward GEMMs to cut B traffic, but the nature of dQ MMA introduces a mismatch. In FlashAttention backward, each CTA owns a fixed KV tile (outer loop parallelized across N CTAs) and iterates over M tiles in the inner loop. The dQ update reduces over the KV sequence in the outer loop. 2-CTA MMA splits the output tile, not the reduction, and the dQ reduction dimension is N, which is already split across the CTA pair. Each CTA still needs the full reduction for the rows it owns.

Solution: DSMEM exchange. We resolve this by exchanging half of dS between the two CTAs using distributed shared memory within the cluster. This repacks dS so it is partitioned along the non-reduction axis: each CTA owns M/2 rows while holding the full 2N reduction. The per-CTA dQ MMA becomes (M/2, 2N)(2N, d), accumulating an (M/2, d) tile in tensor memory. In 2-CTA mode, the S, dP, dV, and dK MMAs keep M=256, while dQ uses M=128 with doubled reduction 2N=256. We then reorder the pipeline to hide DSMEM latency: compute dP for the current tile before computing dQ for the previous tile. Since the dQ tile fits in TMEM alongside P, it can reuse the TMEM region used for S, so dP and dQ no longer share a region as in 1-CTA mode. With this ordering, element-wise dS for the current tile overlaps with the dQ MMA from the previous iteration.

dQ atomic adds. As a side benefit, the dQ decomposition halves the number of global atomic reductions. Atomics are nondeterministic and expensive, and they occur in every inner-loop iteration. Consequently, in the 2-CTA backward pass each CTA writes only half of the dQ tile and performs half as many global atomic reductions as the 1-CTA counterpart.

Deterministic mode

The source of nondeterminism is the global atomic accumulation for dQ. FA4 provides a deterministic mode that serializes the global reductions with a semaphore-style lock and memory fence to enforce a fixed accumulation order. However, determinism does not have to mean “everything stops.” FA4 reduces lock contention with CTA swizzling, and uses a shortest-processing-time-first (SPT) ordering for causal masking to reduce stalls. In practice, deterministic backward reaches up to about 85-90% of the nondeterministic throughput in our benchmarks.

Scheduling

Causal masking and variable sequence length make attention load-imbalanced because different worktiles have different mainloop lengths, so FA4 improves grid linearization and applies longest-processing-time-first (LPT) scheduling to reduce the tail. In fact, these ideas are non-specific to Blackwell or any particular GPU architecture, and we also use them in FA3.

For causal masking, the standard (mblocks, heads, batches) grid order suboptimally processes tiles from shortest to longest, so FA4 swizzles batch-heads into L2-sized sections and traverses the grid by batch-head section, iterating mblocks in reverse order and then the batch-heads within each section.

For variable sequence length, since different batches involve different amounts of work, the given batch-processing order is typically suboptimal from the point of view of the LPT scheduling heuristic. To rectify this, we can launch a preprocessing kernel that sorts batches by maximum per-worktile execution time and writes a virtual-to-actual batch index mapping that the attention kernel uses to traverse batches in sorted order; moreover, the metadata can be cached so that sorting adds no performance loss.

Language and framework: CuTe-DSL

FA4 is implemented entirely in CuTe-DSL, CUTLASS’ Python kernel DSL. Kernels are written in Python; the DSL lowers to PTX, then the CUDA toolkit compiles to GPU machine code. The programming model mirrors CuTe/CUTLASS abstractions with a PTX escape hatch, while cutting compile times by ~20-30x vs C++ templates.

Attention Benchmarks

We show results for FlashAttention-4 on B200 (BF16) and compare it to FlashAttention-2, as well as to implementations in Triton, Gluon, and cuDNN. For cuDNN, we compare against cuDNN 9.13 and the latest version, 9.19.1.2. Starting with versions 9.13 and 9.14, we have worked with the cuDNN team to incorporate some techniques from FlashAttention-4 into cuDNN, so that our work can benefit as many practitioners as possible.

For the forward pass, FlashAttention-4 is 1.1-1.3x faster than cuDNN 9.13 and 2.1-2.7x faster than Triton. For the backward pass, FlashAttention-4 consistently outperforms the other baselines for large sequence lengths.

Since our initial code release 8 months ago, it’s been fun collaborating with the cuDNN and CUTLASS teams at NVIDIA. Newer versions of cuDNN have now implemented many of the optimizations here, and latest cuDNN offers similar perf to FA4.

Acknowledgements

We thank Together AI, Meta, xAI, and Princeton Language and Intelligence (PLI) for compute support. We want to further thank the following teams at NVIDIA: cuDNN, TensorRT-LLM, and CUTLASS teams for constant discussions, ideas, and feedback.

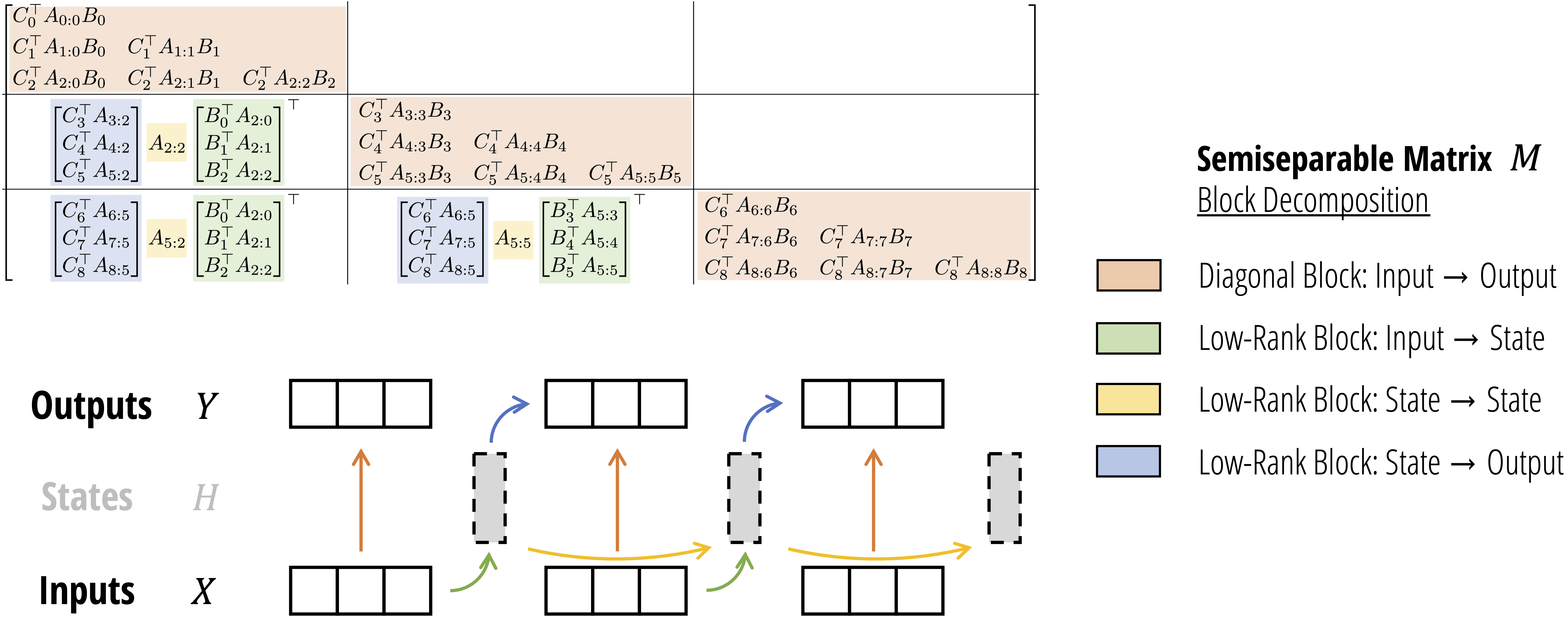
Attention, as a core layer of the ubiquitous Transformer architecture, is a bottleneck for large language models and long-context applications. FlashAttention (and FlashAttention-2) pioneered an approach to speed up attention on GPUs by minimizing memory reads/writes, and is now used by most libraries to accelerate Transformer training and inference. This has contributed to a massive increase in LLM context length in the last two years, from 2-4K (GPT-3, OPT) to 128K (GPT-4), or even 1M (Llama 3). However, despite its success, FlashAttention has yet to take advantage of new capabilities in modern hardware, with FlashAttention-2 achieving only 35% utilization of theoretical max FLOPs on the H100 GPU. In this blogpost, we describe three main techniques to speed up attention on Hopper GPUs: exploiting asynchrony of the Tensor Cores and TMA to (1) overlap overall computation and data movement via warp-specialization and (2) interleave block-wise matmul and softmax operations, and (3) incoherent processing that leverages hardware support for FP8 low-precision.

We’re excited to release FlashAttention-3 that incorporates these techniques. It’s 1.5-2.0x faster than FlashAttention-2 with FP16, up to 740 TFLOPS, i.e., 75% utilization of H100 theoretical max FLOPS. With FP8, FlashAttention-3 reaches close to 1.2 PFLOPS, with 2.6x smaller error than baseline FP8 attention.

The improvements from FlashAttention-3 will result in:

1. More efficient GPU Utilization: The new technique uses up to 75% of an H100 GPU’s maximum capabilities, up from just 35% before. This results in significantly (1.5-2x) faster than previous versions for training and running of large language models (LLMs).
2. Better performance with lower precision: FlashAttention-3 can work with lower precision numbers (FP8) while maintaining accuracy. This allows for even faster processing and potentially lower memory usage, which could lead to cost savings and improved efficiency for customers running large-scale AI operations.
3. Ability to use longer context in LLMs: By speeding up the attention mechanism, FlashAttention-3 enables AI models to work with much longer pieces of text more efficiently. This could allow for applications that can understand and generate longer, more complex content without slowing down.

FlashAttention-3 is available at: https://github.com/Dao-AILab/flash-attention

FlashAttention Recap

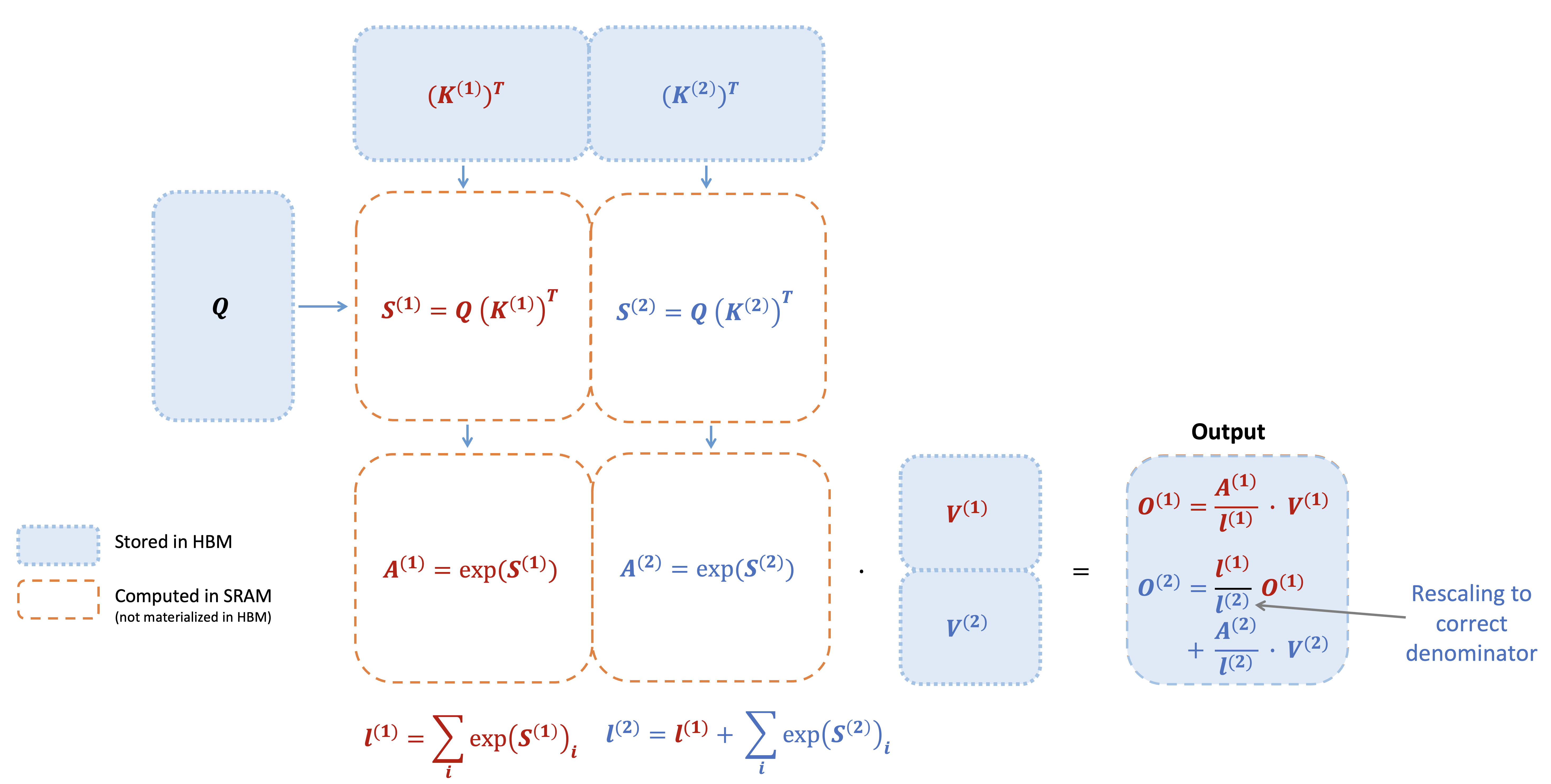
FlashAttention is an algorithm that reorders the attention computation and leverages tiling and recomputation to significantly speed it up and reduce memory usage from quadratic to linear in sequence length. We use tiling to load blocks of inputs from HBM (GPU memory) to SRAM (fast cache), perform attention with respect to that block, and update the output in HBM. By not writing the large intermediate attention matrices to HBM, we reduce the amount of memory reads/writes, which brings 2-4x wallclock time speedup.

Here we show a diagram of FlashAttention forward pass: with tiling and softmax rescaling, we operate by blocks and avoid having to read/write from HBM, while obtaining the correct output with no approximation.

New hardware features on Hopper GPUs - WGMMA, TMA, FP8

While FlashAttention-2 can achieve up to 70% theoretical max FLOPS on Ampere (A100) GPUs, it does not yet take advantage of new features on Hopper GPUs to maximize performance. We describe some of the new Hopper-specific features here, and why they are important.

1. WGMMA (Warpgroup Matrix Multiply-Accumulate). This new feature makes use of the new Tensor Cores on Hopper, with much higher throughputWithout the wgmma instruction, the older mma.sync instruction can only reach about 2/3 the peak throughput of Hopper Tensor Cores: https://arxiv.org/abs/2402.13499v1. than the older mma.sync instruction in Ampere (image from the H100 white paper).

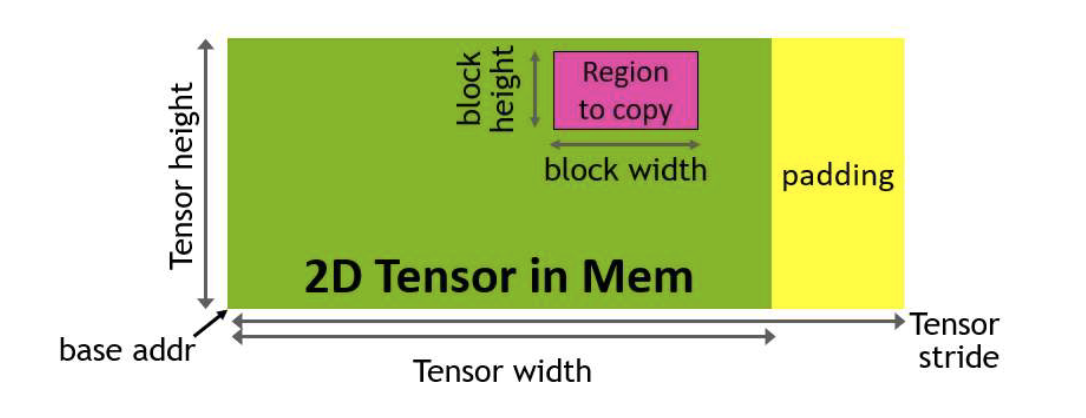
2. TMA (Tensor Memory Accelerator). This is a special hardware unit that accelerates the transfer of data between global memory and shared memory, taking care of all index calculation and out-of-bound predication. This frees up registers, which is a valuable resource to increase tile size and efficiency.

3. Low-precision with FP8. This doubles the Tensor Core throughput (e.g. 989 TFLOPS with FP16 and 1978 TFLOPS with FP8), but trades off accuracy by using fewer bits to represent floating point numbers.

FlashAttention-3 makes use of all of these new features of Hopper, using powerful abstractions from NVIDIA’s CUTLASS library.

Several work such as ThunderKittenThunderKitten also presents an elegant tile-based abstraction for writing fast kernels, you should definite check that out and cuDNN 9 has already shown that these new hardware features can speedup attention computation. By rewriting FlashAttention to use these new features, we can already significantly speed it up (e.g., from 350 TFLOPS in FlashAttention-2 FP16 forward pass to around 540-570 TFLOPS). However, the asynchronous nature of the new instructions on Hopper (WGMMA and TMA) opens up additional algorithmic opportunities to overlap operations and thereby extract even greater performance. For this blogpost, we’ll explain two such techniques specific to attention. The generic technique of warp specialization, with separate producer and consumer warps doing TMA and WGMMA, is well-covered elsewhere in the context of GEMM and works the same here.

Asynchrony: Overlapping GEMM and Softmax

Why overlap?

Attention has GEMMs (those matmuls between Q and K and between attention probability P and V) and softmax as its two main operations. Why do we need to overlap them? Isn’t most of the FLOPS in the GEMMs anyway? As long as the GEMMs are fast (e.g., computed using WGMMA instructions), shouldn’t the GPU be going brrrr?

The problem is that non-matmul operations are much slower than matmul operations on modern accelerators. Special functions such as exponential (for the softmax) have even lower throughput than floating point multiply-add; they are evaluated by the multi-function unit, a unit separate from floating point multiply-add or matrix multiply-add. As an example, the H100 GPU SXM5 has 989 TFLOPS of FP16 matrix multiply, but only 3.9 TFLOPS (256x less throughput) for special functionsThe CUDA programming guide specifies that the throughput for special functions is 16 operations per streaming multiprocessor (SM) per clock cycle. We multiply 16 by 132 SMs and 1830 Mhz (clock speed used to calculate 989 TFLOPS of FP16 matmul) to get 3.9 TFLOPS! For head dimension 128, there are 512x more matmul FLOPS than exponential, which means that exponential can take 50% of the time compared to matmul. The situation is even worse for FP8, where the matmul FLOPS are twice as fast yet exponential FLOPS stay the same speed. Ideally we want matmul and softmax to operate in parallel. While the Tensor Cores are busy with matmul, the multi-function units should be calculating exponential!

Inter-warpgroup overlapping with pingpong scheduling

The first and easiest way to overlap GEMM and softmax is to do nothing at all! The warp schedulers already try to schedule warps so that if some warps are blocked (e.g., waiting for GEMM results), other warps can run. That is, the warp schedulers do some of this overlapping for us, for free.

However, we can improve on this by doing some of the scheduling manually. As an example, if we have 2 warpgroups (labeled 1 and 2 – each warpgroup is a group of 4 warps), we can use synchronization barriers (bar.sync) so that warpgroup 1 first does its GEMMs (e.g., GEMM1 of one iteration and GEMM0 of the next iteration), and then warpgroup 2 does its GEMMs while warpgroup 1 does its softmax, and so on. This “pingpong” schedule is illustrated in the figure below, where the same color denotes the same iteration.

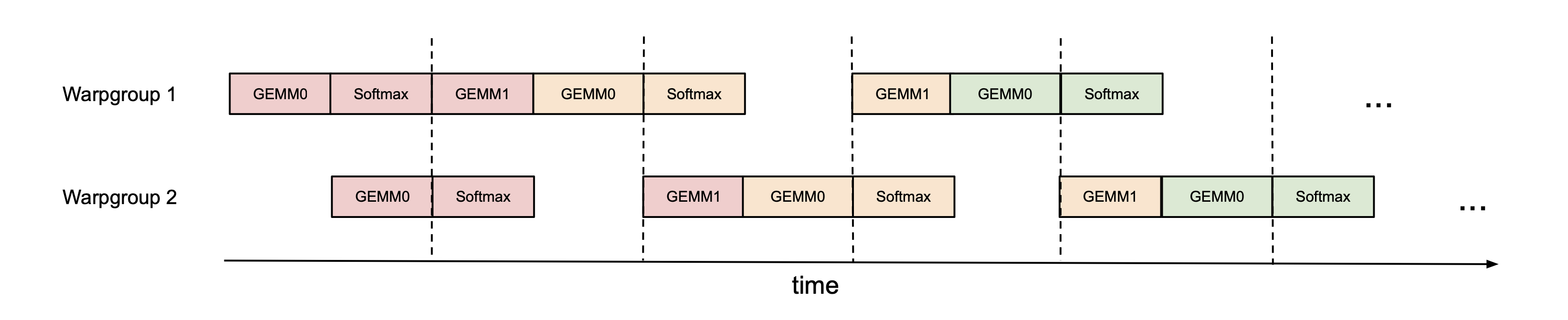
This would allow us to perform the softmax in the shadow of the GEMMs of the other warpgroup. Of course, this figure is just a caricature; in practice the scheduling is not really this clean. Nevertheless, pingpong scheduling can improve FP16 attention forward pass from around 570 TFLOPS to 620 TFLOPS (head dim 128, seqlen 8K).

Intra-warpgroup overlapping of GEMM and Softmax

Even within one warpgroup, we can have some part of softmax running while the GEMMs of that warpgroup is running. This is illustrated in this figure, where the same color denotes the same iteration.

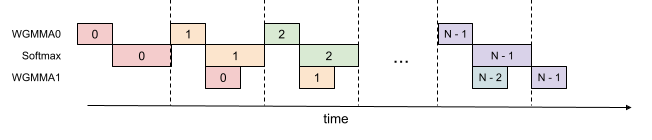
This pipelining increases throughput from around 620 TFLOPS to around 640-660 TFLOPS for FP16 attention forward, at the cost of higher register pressure. We need more registers to hold both accumulators of the GEMMs, and the input/output of softmax. Overall, we find this technique to offer a favorable tradeoff.

Low-precision: reduce quantization error with incoherent processing

LLM activation can have outliers with much larger magnitude than the rest of the features. These outliers make it difficult to quantize, producing much larger quantization errors. We leverage incoherent processing, a technique used in the quantization literature (e.g. from QuIP and QuIP#) that multiplies the query and key with a random orthogonal matrix to “spread out” the outliers and reduce quantization error. In particular, we use the Hadamard transform (with random signs), which can be done per attention head in O(d log d) instead of O(d^2) time, where d is the head dimension. Since the Hadamard transform is memory-bandwidth bound, it can be fused with previous operations such as rotary embedding (also memory-bandwidth bound) “for free”.

In our experiment where Q, K, V are generated from a standard normal distribution but 0.1% of the entries have large magnitudes (to simulate outliers), we found that incoherent processing can reduce the quantization error by 2.6x. We show numerical error comparison in the table below. Please see the paper for details.

Attention Benchmark

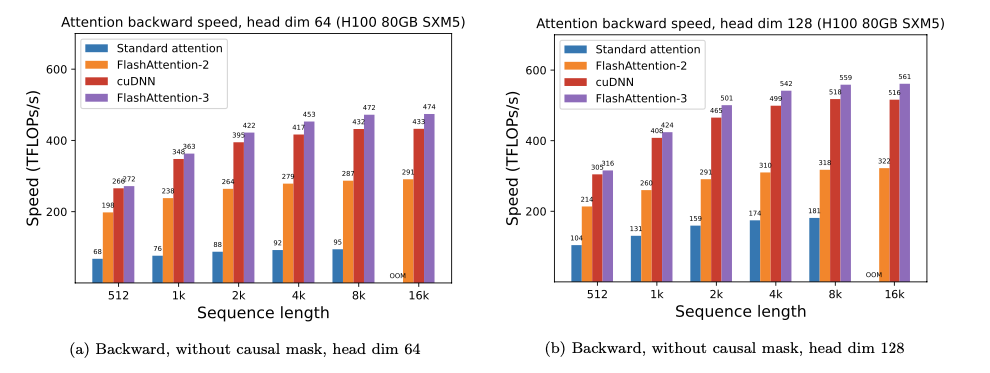
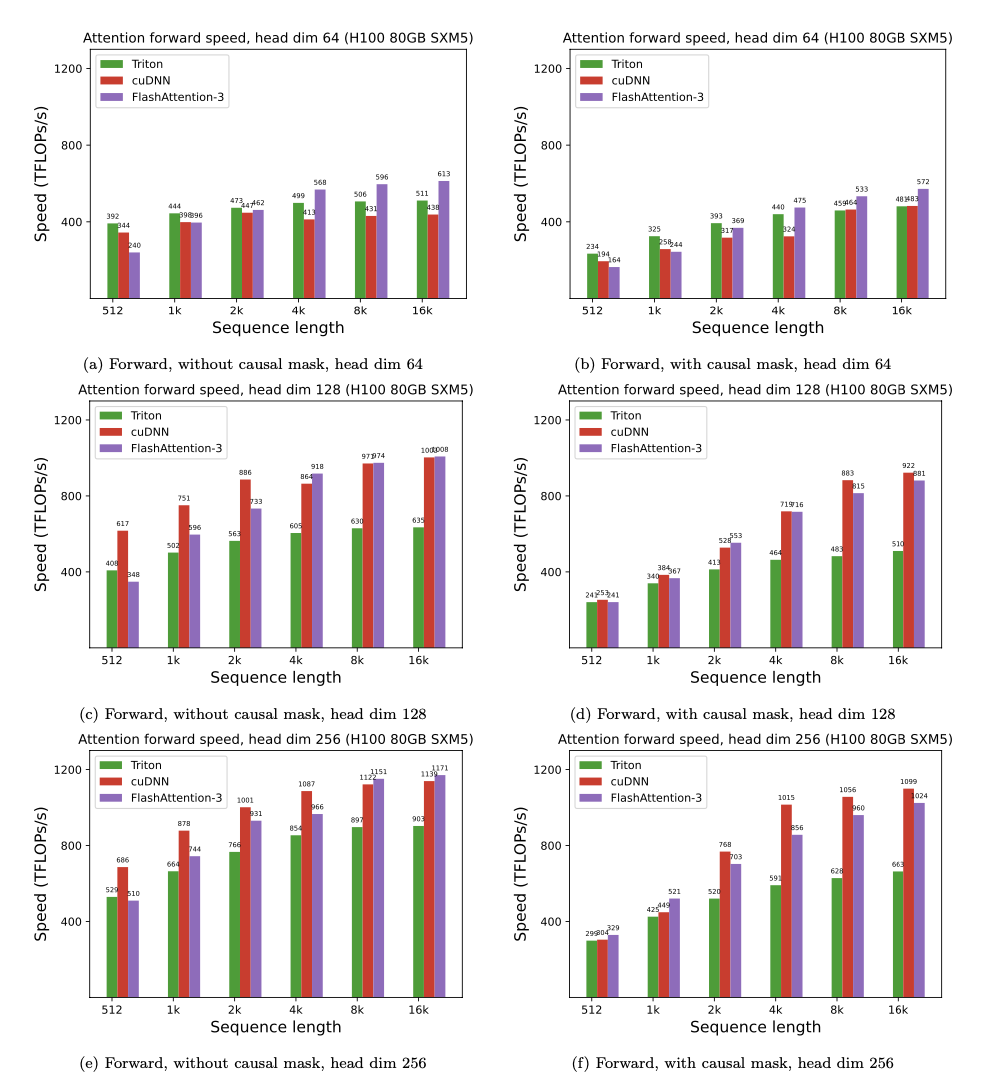
We show some results with FlashAttention-3, and compare it to FlashAttention-2, as well as the implementation in Triton and cuDNN (both of which already use new hardware features of Hopper GPUs).

For FP16, we see about 1.6x-2.0x speedup over FlashAttention-2.

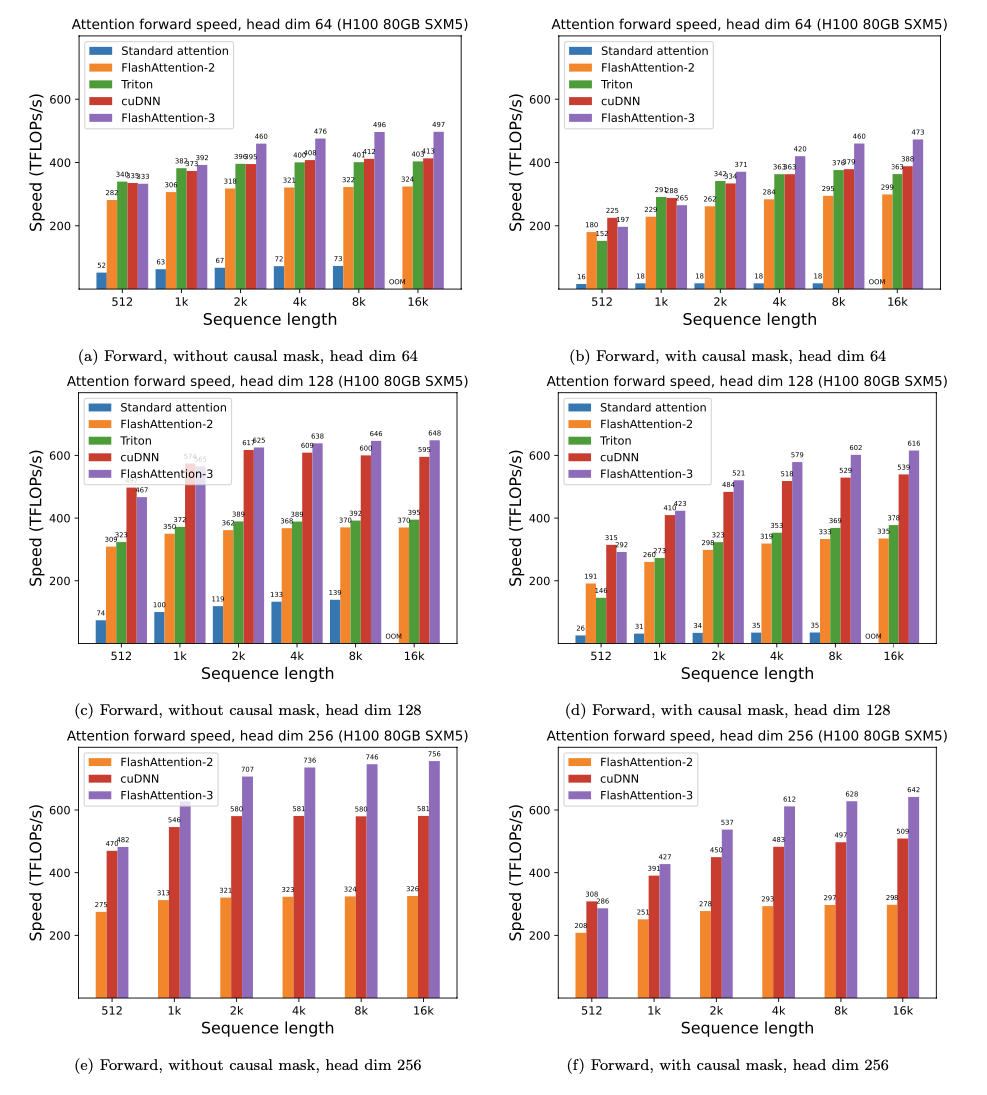
For FP8, we can reach close to 1.2 PFLOPS!

Discussion

This blogpost highlights some of the optimizations for FlashAttention available on Hopper GPUs. Other optimizations (e.g., variable length sequences, persistent kernel, and in-kernel transpose for FP8) are covered in the paper.

We have seen that designing algorithms that take advantage of the hardware they run on can bring significant efficiency gains and unlock new model capabilities such as long context. We look forward to future work on optimization for LLM inference, as well as generalizing our techniques to other hardware architectures. We also look forward to FlashAttention-3 being integrated in a future release of PyTorch.

[Paper] [Code]

This series is cross-posted at GoombaLab

1. Part I - The Model
2. Part II - The Theory
3. Part III - The Algorithm
4. Part IV - The Systems

Since the release of Mamba 6 months ago, we’ve been pleasantly surprised by the overwhelming community response. It’s been incredibly gratifying to see the line of research on efficient sequence models we’ve been pursuing for years really resonate with the machine learning community and take off more than we could have anticipated. We’ve seen an enormous amount of exciting follow-up work, from direct applications (e.g. vision , genomics , graphs , and more) to understanding (e.g. on recall abilities , in-context learning , and formal language expressivity ), and an enormous number of online blogs, tutorials, and videos. We couldn’t be more excited about the direction of this research!

Yet despite its potential so far, we weren’t completely satisfied with the first version of Mamba…

Problem 1 (Understanding)

From a conceptual standpoint, one of the reasons we found SSMs so fascinating is how they just feel fundamental. One way this is exemplified is how they have rich ties to many major paradigms of sequence models. As developed in our earlier works on structured SSMs , they seem to capture the essence of continuous, convolutional, and recurrent sequence models – all wrapped up in a simple and elegant model.

But of course, aside from these, there’s another major sequence model paradigm: variants of the ubiquitous attention mechanism. SSMs always felt somewhat disjoint from attention, and we’ve tried for a while to understand their relationship better.

Question 1: What are the conceptual connections between state space models and attention? Can we combine them?

Problem 2 (Efficiency)

From a computational standpoint, despite the work that went into making Mamba fast (in particular, its hardware-aware selective scan implementation) it’s still much less hardware-efficient than mechanisms such as attention. The missing piece is that modern accelerators such as GPUs and TPUs are highly specialized for matrix multiplications. While this isn’t a problem for inference, which is bottlenecked by somewhat different considerations, this can be a big deal during training time.

Question 2: Can we speed up the training of Mamba models by recasting them as matrix multiplications?

These are the main questions that Mamba-2 – in particular, its new state space model variant – tries to address.

The SSD Model

The main point of the Mamba-2 paper is what we call structured state space duality (SSD), which refers to several things:

1. The SSD model refers to a specific standalone layer, like attention or an SSM, that can be incorporated into deep neural networks
2. The SSD framework is a general framework for reasoning about this model (and many more theoretical connections)
3. The SSD algorithm is an algorithm for computing SSD layers much more efficiently than previous SSMs

The main SSD model or “state space dual model” itself really isn’t so complicated! In this first part of a series of blog posts, we’ll provide a self-contained description of the SSD layer (and Mamba-2) in isolation and how it compares to related models, particularly Mamba-1.

In the next parts of this series, we’ll describe the general framework and theoretical connections, which aren’t necessary to actually use Mamba-2.

The Linear (SSM) Mode

SSD starts from the same set of equations as Mamba:

\begin{equation} \label{eq:ssm} (\text{Selective state space model (SSM)}) \end{equation}

To recap, a structured state space model (SSM) defines a map from $x \in \mathbb{R}^\mathtt{T} \to y \in \mathbb{R}^\mathtt{T}$. Think of $x_t$ and $y_t$ as being scalars, and the hidden state $h_t$ as an $\mathtt{N}$-dimensional vector, where $\mathtt{N}$ is an independent hyperparameter called the state size, state dimension, or state expansion factor.

A selective state space model allows the $(A, B, C)$ SSM parameters to vary across time . We’ll think of them as tensors with shapes $A \in \mathbb{R}^\mathtt{(T, N, N)}$, $B \in \mathbb{R}^\mathtt{(T, N)}$, and $C \in \mathbb{R}^\mathtt{(T, N)}$ respectively.As with Mamba-1, we take everything over the reals $\mathbb{R}$, although complex variants as with other structured SSMs like the S4 lineage are also possible.

Structured SSMs require $A$ to have structure to be efficiently computable, such as the most commonly used diagonal structure . In this case $A$ has shape $\mathtt{(T, N)}$ where only the diagonal elements of the $\mathtt{N} \times \mathtt{N}$ matrices are stored.

SSD: Scalar Structured SSM

The original Mamba (or more precisely its core “S6” layer) is exactly a selective SSM with diagonal structure.

The SSD layer of Mamba-2 makes only one small modification: it restricts the diagonal $A$ even further to a scalar times identity structure; in other words the diagonal elements of $A$ must all be the same value. In this case $A$ can be represented with shape just $\mathtt{(T)}$ and one can also identify $A_t$ as just a scalar (and so we’ll sometimes denote it $a_t$).

Multihead SSMs

Equation \eqref{eq:ssm} is defined only for a single dimensional input $x \in \mathbb{R}^\mathtt{T}$. If $X \in \mathbb{R}^\mathtt{(T, P)}$ has $\mathtt{P}$ separate channels, we can use the same dynamics (i.e. the same SSM $(A, B, C)$) independently for each channel. This can be interpreted as a single head of the SSM model.

Here, we think of $X$ as a tensor of shape $\mathtt{(T, P)}$ where $\mathtt{T}$ is the sequence (time) dimension and $\mathtt{P}$ is the “head dimension”.Normally there's an additional batch dimension $\mathtt{B}$ when implementing these models, which we'll ignore throughout this presentation.

Multiple heads can be constructed completely independently; for the remainder of this post, we assume that we’re working with a single head. Note that these heads are exactly analogous to how heads in multi-head attention models work, and in Mamba-2 we also choose similar dimensions as modern Transformers, e.g. $\mathtt{P} = 64$ or $\mathtt{P}=128$. (To scale to larger model widths $\mathtt{D} = \mathtt{d\_model}$, we keep this fixed and increase the number of independent heads.)

We can notate the general (selective) state space model as \begin{equation} \label{eq:ssm-transformation} Y^\mathtt{(T,P)} = \mathsf{SSM}(A^\mathtt{(T,…)}, B^\mathtt{(T,N)}, C^\mathtt{(T,N)})(X^\mathtt{(T,P)}) \end{equation}

Some axes of variation include

1. The structure on $A$, which affects its parameter shape:
   • ... = (N,N) for general (unstructured) SSMs
   • ... = (N) for diagonal SSMs (or other structures, such as diagonal-plus-low-rank )
   • ... = () for scalar SSMs (i.e. SSD)
2. The state dimension $\mathtt{N}$ (i.e. d_state)
3. The head dimension $\mathtt{P}$ (i.e. d_head)

There are other axes of variation of structured SSMs (e.g. time-invariance vs. selectivity, SISO vs. MIMO, real vs. complex, etc.), but we’re highlighting these so that we can contrast Mamba-2 to Mamba-1 in just a second…

The Quadratic (Attention) Mode

But first, let’s switch tacks and forget about state space models for a moment. Given the same tensors above with the same shapes $(A^\mathtt{(T)}, B^\mathtt{(T, N)}, C^\mathtt{(T, N)})$, let’s define a different object.

First, we’ll define the following matrix (don’t worry, we’ll explain more and give it a name in Part II of this series!)

Then, let’s define the following matrix

\begin{equation} \label{eq:ssd-attention} M = L \circ C B^\top \in \mathbb{R}^{\mathtt{(T,T)}} \end{equation}

Finally, $M$ encodes a sequence transformation $x \in \mathbb{R}^\mathtt{T} \to y \in \mathbb{R}^\mathtt{T}$ mapping a 1D input to a 1D output—just as in equation \eqref{eq:ssm}—through basic matrix multiplication $y = Mx$.

What’s special about this? Well, you may notice that it looks very similar to an attention computation. In fact, if all $a_t = 1$, then $L$ is simply the lower-triangular causal mask and \eqref{eq:ssd-attention} is equivalent to causal linear attention :

This is exactly the same as equation \eqref{eq:ssd-attention} if we rename $(C, B, X) \mapsto (Q, K, V)$!

State Space Duality

The so-called “duality” refers to the fact that the two models defined in equations \eqref{eq:ssm} (for the scalar-identity structured $A_t$ case) and \eqref{eq:ssd-attention} are actually exactly the same model, which we can view as a particular function

In the general SSD Framework (Part II of this series), we’ll show this equivalence in two completely different ways, both of which are actually much more general and each quite illuminating.

If you take our word for it, though, then SSD is relatively simple to contrast in relation to either SSMs or attention.

SSD vs. State Space Models

Compared to previous SSMs, SSD is pretty much the same as the core layer of Mamba but with even more structure on the recurrent $A$ matrices.

1. Mamba-1 (S6) uses diagonal structure on $A$, while Mamba-2 (SSD) uses scalar-times-identity structure on $A$.
2. Mamba-1 has a head dimension of $\mathtt{P}=1$ (i.e. all channels are completely independently controlled by separate SSMs), while Mamba-2 uses a head dimension of $\mathtt{P}>1$ (something like $\mathtt{P}=64$ by default).

In particular, this can be viewed as weight-tied in two ways:

• By restricting the diagonal structure of $A$ to scalar-times-identity, the recurrence dynamics are shared across all $\mathtt{N}$ elements of the state space.
• These dynamics are also shared across all $\mathtt{P}$ channels of a given head.

In other words, a single SSM head has total state size $\mathtt{P} \times \mathtt{N}$, which are each governed by separate scalar recurrences in Mamba-1 but are controlled by a single shared recurrence in Mamba-2.

Why make these restrictions? The main motivation is efficiency: these changes are necessary to be able to view the model in its [dual attention form], which allows matrix multiplications to be used.

The Bottom Line: Mamba-1 vs. Mamba-2

Compared to Mamba-1, Mamba-2 allows much larger state dimensions (from N=16 in Mamba-1 to N=64 to N=256 or even higher in Mamba-2) while simultaneously being much faster during training.

But can this hurt us? There’s some intuition to believe that it shouldn’t. One of the main reasons for the selectivity (e.g. $A$ that depends on the input $X$) introduced in Mamba is to let the SSM be able to control whether to remember or ignore particular pieces of information; for example, if a filler “um” is encountered in a text transcript. But if such information should be ignored, then the entire state can ignore it together, and so it should be okay if the state’s dynamics are shared across all features.

Empirically, we haven’t found evidence that the restricted expressivity of Mamba-2 might hurt, but the jury’s still out! From one perspective, Mamba-2 isn’t strictly better than Mamba-1: while it’s a dramatic improvement from a training perspective, Mamba-1 might be better from a pure inference perspective. Since inference speed of SSMs is entirely governed by the state dimension, if one wants to maximize performance for a target inference efficiency (i.e. for a particular state size $\mathtt{N}$), then the increased expressivity of Mamba-1 might be better. We haven’t fully analyzed the (theoretical or empirical) tradeoffs here, and think this would be a cool direction for the community to dig in more!

SSD vs. Attention

Compared, to standard (self-)attention, SSD also only has two differences:

1. The softmax normalization is dropped.
2. A separate elementwise mask matrix is applied multiplicatively.

The first difference can be interpreted as what reduces the effective state size of the model from linear to constant, and improves its efficiency from quadratic to linear.

The second difference is what distinguishes SSD from standard linear attention. One way to think of the mask is as input-dependent relative positional encodings. Because of the mask $L$ in \eqref{eq:ssd-attention}, the standard attention score $\langle Q_i, K_j \rangle$ is attenuated by a weight

which can be interpreted as a “discount factor” based on how far apart the positions $i$ and $j$ are. (This interpretation was concurrently espoused by Tobias Katsch’s GateLoop paper.) In its attention form, this input-dependent positional mask can be interpreted as the key factor that encodes the “selectivity” of Mamba!

Best of Both Worlds

So why do we care that there are two views of this model? Well, first of all, it’s extremely mathematically interesting, as we’ll cover in Part II, and we hope will inspire future directions. But there are immediate practical benefits too!

Efficiency: the SSM and Attention Modes

The SSM \eqref{eq:ssm} and attention \eqref{eq:ssd-attention} modes represent two different ways of computing the same function, so let’s contrast them.

First, remember that one main reason why SSMs are interesting to begin with is because computing \eqref{eq:ssm} as a recurrence requires maintaining a constant-size state (size $\mathtt{N}$ per channel) and scales linearly in the sequence length $\mathtt{T}$. The downside is that the raw FLOPs don’t reflect actual speed in practice because of hardware considerations…

On the other hand, computing this sequence transformation $y = Mx$ through equation \eqref{eq:ssd-attention} takes quadratic time in the sequence length, because we’re materializing this $\mathtt{T} \times \mathtt{T}$ matrix. But it can be fast in practice because it only uses matrix multiplications, which are extremely optimized on GPUs and TPUs.

Efficiency: the SSD Mode

So if there are two equivalent ways of computing the same model, when should we use one mode or the other? During inference, there’s no trade-off: the SSM mode is designed for fast autoregressive inference. But what about training? Here there’s a tension between FLOPs and hardware efficiency where the attention mode uses more FLOPs, but uses them more efficiently through matrix multiplications.

It turns out we can get the best of both worlds by combining the algorithms! There are two equivalent interpretations of this “state space dual” algorithm, either as

1. A block decomposition of a particular structured matrix that defines the SSD “token-mixing” sequence transformation.
2. A “chunkwise” algorithm that splits the sequence into segments, computes the quadratic attention form on each segment, and adjusts the result by passing the SSM states between segments.

We’ll leave the details of this algorithm to Part III (or Section 6 of the full paper), as it requires a bit of machinery from the theory to derive. But we do emphasize that the implementation of this algorithm isn’t too complicated – a minimal implementation that we provide is only ~30 lines of PyTorch!

The benefits of the SSD algorithm is that it preserves the same efficient FLOP counts as SSMs (compared to quadratic attention), and also dramatically speeds up training compared to general state space models by utilizing matmuls.

The Mamba-2 Architecture

Although the core contribution of Mamba-2 is the new SSD layer and theory, we also make some small changes to Mamba’s neural network architecture.

The main change is producing the $(A, B, C)$ SSM parameters in parallel with the $X$ input, instead of sequentially. This is partly motivated by the connections to attention; but more pragmatically, it’s simpler and more amenable to scaling techniques such as tensor parallelism, which will be discussed in Part IV of this series!

There are some other small differences which are covered in more detail in the paper. However, we do want to emphasize that these architectural changes aren’t really the main point of the model.

Language Modeling

In terms of empirical results, we didn’t test Mamba-2 as extensively as Mamba-1, but believe it should generally be on par or better across the board. Our full language model results use the same protocol as Mamba, and found slightly better scaling at Chinchilla laws .

Fully trained models on the Pile dataset and the standard zero-shot downstream evaluations show similar trends. We emphasize that even when the performance is comparable, Mamba-2 is much faster to train than Mamba-1!

Synthetic Language Modeling: MQAR

More interestingly, we highlight the one synthetic task we tried. Since the original Mamba paper, which investigated synthetics such as Synthetic Copying and Induction Heads, many follow-up works have begun investigating harder associative recall tasks. The multi-query associative recall (MQAR) task introduced by the Zoology and Based line of work has become a de facto standard.

We ran a version of this task that’s much harder than the one usually reported in the literature, and found that Mamba-2 is substantially better than Mamba-1. One reason for the improved performance is the much larger state size (up to $16\times$ larger than Mamba-1 here), which was one of the primary motivations of Mamba-2 in the first place.

Interestingly, Mamba-2 also appears to be noticeably better than Mamba-1 on this particular task even when the state size is controlled. We’re not quite sure why to be honest, and it would be great to ablate the other aspects of the model to investigate… for example, could it be possible that the [restricted structure of SSD] is actually helpful here?

Next Up

In the next part of this series, we’ll go more into the full SSD framework, including how to prove the claimed “duality” of the SSD layer, and strong generalizations of it.

In Part I of this series, we defined the state space dual (SSD) model. In isolation, this model is relatively simple to define, and we claimed that it can be computed either as an SSM recurrence or with an attention-like pattern. If you just want to use the model, feel free to skip this post!

In this post, we’ll dive into the theory behind the model. We’ll derive the SSD “duality” in two completely separate ways, one starting from the SSM perspective and one from the attention perspective. Each method is actually much more broad than the SSD model itself, and the union of these two strong generalizations is what we call the SSD framework. This framework provides a rich body of connections between state space models, attention, and structured matrices. While the SSD model can be viewed as a specific instantiation of each prong of the framework, the SSD framework is much more general opens up many directions for future work.

The State Space Duality framework

For each of the two parts of this framework, we’ll

1. Define the general concepts
2. Show how the SSD model is an instantiation, and prove the duality
3. Suggest future directions for how the framework can be used

Note that this theory is not necessary to use the SSD model itself; this part of the series can be safely skipped for the practitioner that just wants to use SSD (Mamba-2).

Recap: The SSD Model

Part I of this series introduced the SSD layer, which is defined as a selective SSM

\begin{equation} \label{eq:ssm} (\text{Selective state space model (SSM)}) \end{equation}

with scalar-identity structure on $A$.

More formally, we view it as a sequence transformation $X \mapsto Y$

\begin{equation} \label{eq:ssm-transformation} Y^\mathtt{(T,P)} = \mathsf{SSM}(A^\mathtt{(T)}, B^\mathtt{(T,N)}, C^\mathtt{(T,N)})(X^\mathtt{(T,P)}) \end{equation}

The dual attention-like form of the SSD layer is

\begin{equation} \label{eq:ssd-attention} M = L \circ C B^\top \in \mathbb{R}^{\mathtt{(T,T)}} \end{equation}

Now let’s see how to prove this!

SSD Framework 1: Structured Matrix Transformations

The first framing of the duality will be from an SSM-centric perspective, where we’ll prove the duality through the framework of matrix sequence transformations or “matrix mixers”.

Matrix Transformations

The idea is that many sequence models, i.e. sequence transformations $X \in \mathbb{R}^\mathtt{(T,P)} \mapsto Y \in \mathbb{R}^\mathtt{(T,P)}$, can be written in the form of a single matrix multiplication $Y = M(X) \cdot X$ where $M$ is a matrix which can itself depend on $X$. We call this a matrix sequence transformation, or matrix transformation for short. In the literature sequence transformations have also been referred to as “sequence mixers” or “token mixers”, and matrix sequence transformations as “matrix mixers”. There are many examples of these, which are distinguished by the structure of the $M$ matrix. The de facto example is self-attention itself, where $M = \mathsf{softmax}(QK^\top)$ is the attention matrix. Other examples include MLP-Mixer, FNet, and Monarch Mixer.

Why do we care about these types of models?

Writing a sequence model as a matrix transformation provides a powerful tool to understand the structure and characteristics of the model.

And although general non-linear RNNs such as LSTMs cannot be written as matrix mixers, state space models can! In fact, this is pretty easy to see by just unrolling the definition of the SSM recurrence. The upshot is that the SSM \eqref{eq:ssm-transformation} can be written as a matrix transformation

where $M_{ij} = 0$ for $i < j$ (i.e. it’s lower triangular) and otherwise \begin{equation} \label{eq:semiseparable} M_{ij} = C_i^\top A_{i:j}^\times B_j := C_i^\top A_i \dots A_{j+1} B_j \end{equation}

Drawing it out, this matrix looks like

\begin{equation} \label{eq:ssm-matrix} (\text{Matrix Transformation Representation of State Space Models}) \end{equation}

Semiseparable Matrices

This type of matrix in fact has a name: it’s called a (triangular) semiseparable matrix, and has been studied in other fields of engineering and computational linear algebra. These matrices are (IMO) quite fundamental and beautiful, and the full paper talks about more of their properties. For example, an alternative characterization of semiseparable matrices is their structured rank property, which says that every submatrix contained in the lower-triangular portion is low rank.

For our purposes, we’ll care about this form mainly for the algorithmic considerations. One of the central messages of this SSD paper is that:

Takeaway: Computing SSMs Through Matrix Multiplication

All algorithms for computing state space models can be viewed as structured matrix multiplication algorithms on semiseparable matrices.

Let’s see an easy instantiation of this, focusing on our main objective!

Deriving the Duality: SSM to Attention

To show that equation \eqref{eq:ssd-attention} follows from equation \eqref{eq:ssm} (in the case of the SSD model, i.e. scalar SSM), we directly use the matrix form of the state space model \eqref{eq:semiseparable}. Because the $A_t$ are all scalars in this case, they can be factored out of the entries

which directly implies equation \eqref{eq:ssd-attention}.

In summary:

Duality Representation 1 (SSM)

The duality for the SSD model can be seen as two different matrix multiplication algorithms on the semiseparable matrix.

• The linear form is a structured matrix multiplication algorithm that computes the outputs $Y_0, Y_1, \dots$ sequentially, leveraging the structure of the semiseparable matrix.
• The quadratic form is the naive matrix multiplication algorithm that materializes the full matrix.

Going Beyond the SSD Layer 1

The power of the semiseparable matrix representation applies to all state space models, with various downstream implications.

Algorithms

Algorithmically, the Mamba-2 paper explores several consequences, such as:

1. The above duality result for the SSD model, i.e. a scalar-identity structured SSM.
2. New asymptotic efficiency results for state space models (Theorem 3.7), which follow from applying known results from the semiseparable matrix literature .
3. A more general hybrid algorithm that can be viewed as combining both the linear and quadratic forms to get the best of both worlds. This can be derived as a new matrix multiplication algorithm utilizing block decompositions of the semiseparable matrix. This is the subject of Part III of this blog series!

Understanding

Conceptually, the matrix transformation viewpoint helps provide a unifying view of sequence models. Some example downstream ideas include

• New sequence models: Restricting ourselves to matrix transformations reduces the problem of developing new sequence models to that of finding structured matrix classes with target properties. In ongoing work by my students, we study this point of view, and use it to derive the most natural bidirectional extension of Mamba (coming very soon!).
• Expressivity: Looking at the matrix transformation representation can help us understand what different models can represent from a linear algebraic perspective. In another ongoing work, we use this as a tool to study which subquadratic models are the most amenable to being distilled from Transformers.
• Interpretability: A concurrent work derived the matrix formulation of SSMs and use it to probe the internal representations of Mamba models.

We’re excited to see what algorithmic and conceptual ideas from the structured matrix literature can be applied to further improve state space models!

SSD Framework 2: Structured Attention

The second framing of the duality is from an attention-centric perspective, where we’ll prove the duality through the framework of tensor contractions.

Note that this is entirely independent of the previous [matrix transformation viewpoint].

Warm-up: Kernel Attention

For our purposes, we’ll define attention as a function

given by the pairwise matrix multiplications

We’ll restrict ourselves to the case when $\psi$ is finite, which is sometimes called kernel attention. Many, many variants have been proposed before!

Why do we care about this formulation? When the sequence length $\mathtt{T}$ grows and the feature dimension $\mathtt{N}$ is small—commonly, in the regime when $\psi$ is simple such as an elementwise transform and so $\mathtt{N}$ is constant—then the cost of attention can be reduced from quadratic in $\mathtt{T}$ to linear. This follows from simply computing the matrix multiplications in a different order

This is a somewhat “folklore” interpretation of linear attention.At least, one lineage of efficient attention; other varieties exist, such as those based on sparsity or hashing. We reserve the term "linear attention" to those related to Katharopoulos et al., or more broadly low-rank attention.

The most common way of linearizing attention is usually viewed as a consequence of the associativity of matrix multiplication

(Causal) Linear Attention

However, once the basic kernel attention is slightly modified, we can no longer use the associativity of matrix multiplication directly.

The seminal Linear Attention (LA) framework of Katharopoulos et al. shows that it can still be extended to the important case of incorporating causality into attention, for autoregressive settings such as language modeling.

Let’s be a lot more explicit about how it works. The quadratic form of causal linear attention is \begin{equation} \label{eq:quadratic-kernel-attention} Y = (L \circ QK^\top) \cdot V \end{equation} where

is the causal mask matrix.

The issue is: once the $L$ mask is incorporated into \eqref{eq:quadratic-kernel-attention}, we can no longer directly apply matrix associativity! This is the problem that the original Linear Attention paper addresses. What they show is that \eqref{eq:quadratic-kernel-attention} is equivalent to a different form which avoids materializing the quadratic $QK^\top$ attention matrix and has linear time complexity

As far as we’re aware this wasn’t explicitly proved in the paper, although it isn’t too hard to write out the summation to show it.

What we’ll do is prove this equivalence in essentially one line, while revealing exactly where the “linear” part of Linear Attention comes from, and how to strongly generalize it.

Spoiler alert:

Where does the cumsum in Linear Attention come from?

The appearance of the cumulative sum in linear attention is exactly equivalent to the fact that the causal mask $L$, as a matrix multiplication, encodes cumulative sums:

\[y = L \cdot x \iff y = \mathsf{cumsum}(x)\]

A Tensor Contraction Proof of Linear Attention

Let’s write out the quadratic form of linear attention \eqref{eq:quadratic-kernel-attention} very explicitly in tensor contraction or einsum notation, with shape annotations:

\begin{equation} \label{eq:sma-quad} (\text{Structured Masked Attention - Quadratic Form}) \end{equation}

With this notation, we can notice that this sequence of contractions can be written as a single four-way contraction

\begin{equation} \label{eq:sma} y = \mathsf{contract}(\mathtt{TN},\mathtt{SN},\mathtt{SP},\mathtt{TS} \to \mathtt{TP})(Q, K, V, L) . \end{equation}

And finally, it can be computed with any other contraction ordering. In particular, we can perform pairwise reductions on the order $V, K, L, Q$ instead of $Q, K, L, V$

\begin{equation} \label{eq:sma-lin} (\text{Structured Masked Attention - Linear Form}) \end{equation}

Now the key observation is that the second line of \eqref{eq:sma-lin} is simply a matrix multiplication by $L$, which can be computed with a cumulative sum.

That’s the entire proof of linear attention! The beauty of it is that we didn’t have to write out a single summation, which was abstracted out into a tensor contraction combined with the structure of $L$.

This immediately proves our claim about the cumsum in linear attention. Moreover, this immediately reveals that the efficiency of linear attention can be made much more general…

Structured Masked Attention

The critical observation is that in order for \eqref{eq:sma-lin} to be fast, all that is necessary is for $L$ to be any structured matrix – in other words any matrix that has subquadratic matrix-vector multiplication.

This immediately motivates one of the main prongs of the SSD framework, which can be seen as a strong generation of LA.

Definition: Structured Masked Attention

Structured masked attention (SMA) is defined as the four-way tensor contraction \eqref{eq:sma} using an attention mask $L$ that is a structured matrix.

Duality Representation 2 (SMA)

SMA has dual quadratic and linearAssuming that the structured matrix $L$ has linear time matrix-vector multiplication modes which are simply two different pairwise reduction orders \eqref{eq:sma-quad} and \eqref{eq:sma-lin}.

Finally, let’s just connect this back to the commonly held view of linear attention as matrix multiplication associativity.

Although it is commonly believed that incorporating attention masks $L$ prevents matrix multiplication reordering, it turns out to still be compatible. In particular, associativity of matrix multiplication is a special case of tensor contraction reduction orders; although the former no longer applies, the latter can integrate the attention mask $L$.

Next, let’s look at some consequences of the structured attention framework.

Deriving the Duality: Attention to SSM

Recall that the SSD model is defined as either a scalar-identity SSM in equation \eqref{eq:ssm}, or through the attention-like form in equation \eqref{eq:ssd-attention}.

To show the equivalence of these forms, we simply recognize that \eqref{eq:ssd-attention} is a special case of structured masked attention where the mask matrix is

\begin{equation} \label{eq:1-ss} (\text{1-semiseparable (1-SS) matrix}) \end{equation}

We call this a 1-semiseparable (1-SS) matrix, for reasons that are explained in more detail in the Mamba-2 paper.

Thus, we can also say that the SSD model is 1-semiseparable masked attention or 1-SS SMA.

To prove that this can be written as an SSM, we simply appeal to the SMA framework, which says that the dual form of this model can be computed through matrix multiplication by $L$. So how fast is that? It’s not too hard to see that multiplication $y = Lx$ can be computed in linear time through a scalar recurrence:

This corresponds exactly to the original SSM recurrence!

(In fact, multiplication by 1-SS matrices $L$ can be computed in a lot more ways, which we compile in the full paper! Alternative algorithms can reveal more insights: for example, the associative scan algorithm used by S5 and Mamba can also be shown to be a structured matrix multiplication algorithm on 1-SS matrices.)

Going Beyond the SSD Layer 2

Structured masked attention not only helps define the SSD model and prove its duality, but it is a much broader framework of efficient attention models.

Prior examples include the original linear attention as well as the recent Retentive Network (RetNet) model. These can be viewed as direct special cases of SSD. But beyond SSD, we can define classes of efficient attention by replacing the mask $L$ with any structured matrix. As a suggestion, we think that Toeplitz or Fourier structured attention may be interesting to consider because they might encode different forms of positional information.

Additionally, other forms of structure can be incorporated into the $L$ mask. For example, another extension my students are developing is viewing SSD (and recurrences in general) as an algorithm operating on directed line graphs, and generalizing it to incorporate arbitrary graph structures.

State Space Duality

We’ll end this post with a brief recap of what we’ve covered.

The SSD framework consists of the two broad approaches covered in this post, which is summarized by the two areas of the [Venn diagram]:

1. Viewing state space models through [structured matrix transformations]
2. Generalizing linear attention through [tensor contractions]

The [SSD layer] is a particular model which is the purple intersection in the figure, which can be viewed as an instance of either part of the SSD framework, and in particular has dual quadratic and linear forms that can be derived from either representation.

Next Up

In the next part of this series, we’ll see how to use some of the SSD framework (in particular, the structured matrix algorithm point of view) to derive the more efficient hybrid SSD algorithm that leverages both of the dual forms.

The theoretical framework of structured state space duality (see Part I and Part II of this series) connects SSMs and (linear) attention through structured matrices. As mentioned in Part I, this connection allows us to derive new algorithms for selective SSMs that are faster than the parallel associative scan in Mamba-1 by leveraging matrix multiplication as a primitive. Moreover, the connection can bring system optimizations (e.g. tensor parallelism, sequence parallelism, variable sequence length) originally developed for Transformer to SSM-land.

The SSD Algorithm

Even though we already developed optimized scans implementations for Mamba-1, we were limited to small state expansion (typically $\mathtt{N}=16$) as the algorithm and implementation did not use tensor cores (specialized hardware units that perform matrix multiplication). Typically matrix multiplication (matmul) FLOPs are much faster (up to 16x) than non-matmul FLOPs: the A100 GPU has 312 TFLOPS of BF16 matmul but only 19 TFLOPS of FP32 arithmetics, and the H100 has 989 TFLOPS of BF16 matmul but only 67 TFLOPS of FP32 arithmetics. One of our primary goals with Mamba-2 is to leverage tensor cores to speed up the SSM.

To recap, after tying parameters and introducing the head structure, the SSM in Mamba-1 turns into SSD, a more restrictive form that has an attention-like formulation. And as SSD connects SSMs and structured matrices, we saw in Part II that efficient algorithms to compute SSMs correspond directly to different decompositions of the “token-mixing” or “sequence-mixing” matrix $M$.

We can therefore create new algorithms to compute SSMs simply by looking for alternative ways to multiply this matrix, for example by decomposing it in various ways. A simple block decomposition of this matrix, with carefully chosen block sizes, turns out to get all the advantages of both the linear-recurrent and quadratic-attention dual forms of SSD. This leads to the SSD algorithm, which has 4 steps. There are two completely different interpretations of this algorithm!

SSD Algorithm: Block Matrix Decomposition

We first partition the SSM (semiseparable) matrix into blocks of size $\mathtt{Q} \times \mathtt{Q}$. Then, we use the properties of semiseparable matrices to factorize each off-diagonal block, which is low rank.

1. (Orange) Each diagonal block is a smaller semiseparable matrix; we can compute this multiplication however we like; in particular, using the quadratic (attention-like) form of SSD.
2. (Green) There are only $\mathtt{T} / \mathtt{Q}$ total different green blocks because many of them are shared. These can be computed with a batched matmul.
3. (Yellow) Notice that the yellow terms themselves form a 1-semiseparable matrix; in other words, this step is equivalently to an SSM scan (on some modified $A$ factors)!
4. (Blue) Similar to green, these can be computed with a batched matmul.

SSD Algorithm: Chunking and State Passing

An alternative interpretation of the algorithm involves reasoning about how the SSM operates on the actual sequence. We first split the sequence of input into blocks (or chunks) of size $\mathtt{Q}$. The steps then have the interpretation

1. Intra-chunk outputs: compute the local output of each chunk (what is the output per chunk supposing that the initial state (to the chunk) is 0?)
2. Chunk states: compute the final state of each chunk (what is the final state per chunk supposing that the initial state (to the chunk) is 0?)
3. Pass states: compute a recurrence on all of the chunks’ final states – using any desired algorithm, e.g. parallel or sequential scan (what is the actual final state per chunk taking into account all previous inputs?)
4. Output states: for each chunk, given its true initial state (computed in Step 3), compute the contribution to the output just from the initial state

Either way, we see that most of the algorithm (Step 1, 2, and 4) leverages matmuls (and hence tensor cores), and also can be computed completely in parallel! Only Step 3 requires a scan, but it operates on a much shorter sequence and usually only takes a small fraction of the time of the full algorithm.

Special Cases

We note that special cases of this algorithm have been seen before. In particular RetNet, which we showed in Part II to be a special case of SSD, mention a “chunkwise” algorithm which computes the quadratic form on a chunk of the input one-at-a-time and passes the final state to the next chunk. This turns out to be essentially equivalent to the SSD algorithm specialized to a restricted case (i.e. a decay matrix mask $L$). Our derivation comes from a different direction—the block matrix decomposition—which also makes it more obvious how to parallelize this algorithm and make it really fast in practice.

Other forms of “chunkwise” recurrences have recently become popular, such as in Gated Linear Attention (GLA).

The Code

In the “Minimal SSD” code that we provide in the paper and the code release, we delineate each of these four steps. As promised, this algorithm is not only faster but also much easier to implement than the original selective scan of Mamba, coming in at just around 25 lines of code!

def segsum(x):
    """Naive segment sum calculation. exp(segsum(A)) produces a 1-SS matrix,
       which is equivalent to a scalar SSM."""
    T = x.size(-1)
    x_cumsum = torch.cumsum(x, dim=-1)
    x_segsum = x_cumsum[..., :, None] - x_cumsum[..., None, :]
    mask = torch.tril(torch.ones(T, T, device=x.device, dtype=bool), diagonal=0)
    x_segsum = x_segsum.masked_fill(~mask, -torch.inf)
    return x_segsum

def ssd(X, A, B, C, block_len=64, initial_states=None):
    """
    Arguments:
        X: (batch, length, n_heads, d_head)
        A: (batch, length, n_heads)
        B: (batch, length, n_heads, d_state)
        C: (batch, length, n_heads, d_state)
    Return:
        Y: (batch, length, n_heads, d_head)
    """
    assert X.dtype == A.dtype == B.dtype == C.dtype
    assert X.shape[1] % block_len == 0

    # Rearrange into blocks/chunks
    X, A, B, C = [rearrange(x, "b (c l) ... -> b c l ...", l=block_len) for x in (X, A, B, C)]

    A = rearrange(A, "b c l h -> b h c l")
    A_cumsum = torch.cumsum(A, dim=-1)

    # 1. Compute the output for each intra-chunk (diagonal blocks)
    L = torch.exp(segsum(A))
    Y_diag  = torch.einsum("bclhn,bcshn,bhcls,bcshp->bclhp", C, B, L, X)

    # 2. Compute the state for each intra-chunk
    # (right term of low-rank factorization of off-diagonal blocks; B terms)
    decay_states = torch.exp((A_cumsum[:, :, :, -1:] - A_cumsum))
    states = torch.einsum("bclhn,bhcl,bclhp->bchpn", B, decay_states, X)

    # 3. Compute the inter-chunk SSM recurrence; produces correct SSM states at chunk boundaries
    # (middle term of factorization of off-diag blocks; A terms)
    if initial_states is None:
        initial_states = torch.zeros_like(states[:, :1])
    states = torch.cat([initial_states, states], dim=1)
    decay_chunk = torch.exp(segsum(F.pad(A_cumsum[:, :, :, -1], (1, 0))))
    new_states = torch.einsum("bhzc,bchpn->bzhpn", decay_chunk, states)
    states, final_state = new_states[:, :-1], new_states[:, -1]

    # 4. Compute state -> output conversion per chunk
    # (left term of low-rank factorization of off-diagonal blocks; C terms)
    state_decay_out = torch.exp(A_cumsum)
    Y_off = torch.einsum('bclhn,bchpn,bhcl->bclhp', C, states, state_decay_out)

    # Add output of intra-chunk and inter-chunk terms (diagonal and off-diagonal blocks)
    Y = rearrange(Y_diag+Y_off, "b c l h p -> b (c l) h p")
    return Y, final_state

The Details

Let’s talk about a couple of additional details in the implementation (these don’t even appear in the full paper, so pay attention!) that unpack some of the choices in this reference code.

The SSM Scan

In the above code, we utilized the connection between scalar SSM recurrences

and matrix multiplication by 1-semiseparable matrices

which we covered in Part II (and Section 3.2.2 of the paper). In this minimal implementation, we compute Step 3 of the algorithm, which is computing a scalar SSM by any algorithm of our choice, by explicitly materializing a 1-SS matrix and doing dense matrix multiplication.

We use this version for several reasons:

1. Code-wise, it’s simpler to materialize and multiply by this matrix than to actually implement a parallel associative scan
2. Because of the block decomposition of the SSM matrix, the sequence length $\mathtt{T}$ is reduced by a factor of $\approx 100$ – so doing the scan in time $O(\mathtt{T}^2)$ instead of $O(\mathtt{T})$ isn’t too bad
3. We have to materialize a 1-SS matrix anyways for Step 1 of the algorithm (the diagonal blocks), so might as well reuse the code ¯\_(ツ)_/¯

While this example code is simpler and reasonably efficient on GPU (and probably TPU as well!), it’s no longer truly linear at long sequences. Our more optimized Triton implementation does replace the 1-SS multiplication in Step 3 with an actual associative scan.

Stability

Attempt 1: Ratios of cumprods

The first naive attempt may be to notice that the entries of this matrix are cumulative products

However, this runs into severe numerical issues because these products can get really tiny (imagine $a_t \approx 0.9$ and powering it up for a sequence length $\mathtt{T}$ in the thousands!)

Fix 1: The Segment Sum (segsum) Operation

The second attempt would be to do all of this in log-space, because all the $a_t$ are positive; so the products become additions, and instead of cumprods to deal with we have cumsums instead. Then in order to compute the 1-SS matrix, we just have to compute the sums $\log a_i + \dots + \log a_{j-1}$ for every segment $[i:j]$. We call this the segment sum (segsum) primitive, analogous to cumulative sum (cumsum).

Attempt 2: Differences of cumsums

The obvious way to do this again is using the same idea as above, but in log space

where we compute a single cumulative sum of $a$ along the time axis, and then compute all pairwise differences. In code, we can do this with

def segsum_unstable(x):
    """Naive segment sum calculation."""
    T = x.size(-1)
    x_cumsum = torch.cumsum(x, dim=-1)
    x_segsum = x_cumsum[..., :, None] - x_cumsum[..., None, :]
    mask = torch.tril(torch.ones(T, T, device=x.device, dtype=bool), diagonal=0)
    x_segsum = x_segsum.masked_fill(~mask, -torch.inf)
    return x_segsum

(and then the 1-semiseparable matrix is just the exponential of this output).

Sums/differences are a lot more stable than products/quotients, so this should work – right?

Fix 2: Remove All Subtractions

Unfortunately, it turns out this still doesn’t work. The values of this 1-SS matrix roughly represent the SSM dynamics, which are very sensitive to these values of $a_t$, so we have to be very precise. And even in log space, these cumsums can be fairly large, which runs into catastrophic cancellation when subtracted. So we really have to find a way to compute this matrix with only additions, while still vectorizing everything…

Attempt 3: Stable Segsum

This leads to the helper function in the reference SSD code. Instead of computing a single cumsum and then subtracting, we find a way to use a batch of independent cumsums that immediately produces the right answer without subtraction.

These details do matter! Without the right implementation of these primitives, the basic SSD algorithm produces NaNs immediately during training (even with FP32).

Discretization

This lineage of structured state space models developed from S4 and its predecessors which were viewed as continuous-time systems.

In Mamba, however, we don’t really view the SSM as continuous anymore. In fact, as mentioned in the Discussion (Section 5) of the original paper, Mamba trades off with S4 on modeling different types of data:

• S4 is a continuous-time model that excels at modeling continuous data, e.g. perceptual signals such as audio waveforms and pixel-level vision.
• Mamba is a discrete-time model that excels at modeling discrete data, e.g. tokenized data such as language.

However, the parameterization of Mamba still used the same discretization step as in prior structured SSMs, where there is another parameter $\Delta$ being modeled. We do this because the discretization step has other side effects such as properly normalizing the activations which is important for performance.

The initializations and parameterizations from the previous theory on structured SSMs still work out-of-the-box, so why fix what’s not broken?

Despite this, we’re pretty sure that the discretization step isn’t really necessary for Mamba. In the Mamba-2 paper, we chose to work directly with the “discrete parameters” $A$ and $B$, which in all previous structured SSM papers (including Mamba-1) were denoted $(\bar{A}, \bar{B})$ and defined through an additional transformation

This doesn’t pose any problems: to use the continuous SSM parameterization, simply transform the parameters through the above formulas before plugging into the SSD code above.

In the full Mamba-2 code, we also kept the same parameterization and discretization step as in Mamba—again, why fix what’s not broken?—but hypothesize that “discrete-centric” variants (such as the gamma normalization of LRU and Griffin) should work equally well.

Is Discretization Necessary?

It’s useful for other structured SSMs, but perhaps not needed for Mamba. But it’s just a simple invertible transformation, so use either discrete or continuous parameterizations as you like!

What’s Next

In the final part of this series, we’ll continue talking about the implementation of Mamba-2, but on a more macroscopic level; about the entire neural network, instead of just details of the core SSD layer.

We’ll also talk about the actual speed of the algorithm covered in this post.

Transformers have benefited from 7 years of systems optimization from the whole research community and large companies. The SSD framework draws connections between SSMs and attention, and allows us to implement many of these optimizations for models like Mamba-2 as well. We focus on tensor parallel and sequence parallel for large-scale training, as well as variable-length sequences for efficient finetuning and inference.

Systems and Scaling Optimizations

Tensor Parallelism

One difficulty with large-scaling training of Mamba-1 using tensor parallelism (TP) is that it requires 2 all-reduces per layer, compared to just 1 all-reduce per attention or MLP layer in Transformer. This is because some of the SSM parameters are functions of the inner activations, not of the input to the layer. In Mamba-2, with the “parallel projection” structure, all SSM parameters are functions of the input to the layer, and we can easily apply TP to the input projection: We split the input projection and output projection matrices into 2, 4, 8 shards, depending on the TP degree. We use a grouped norm with number of groups divisible by the TP degree, so that normalization is done separately per GPU. These changes result in 1 all-reduce per layer, instead of 2.

Sequence Parallelism

When training on very long sequence length, we might need to split along the sequence length and assign different parts to different devices. There are two main forms of sequence parallelism (SP): For the residual and normalization operation: this replaces the all-reduce in TP with a reduce-scatter, residual + normalization, then all-gather. Since Mamba-2 uses the same residual and normalization structure as Transformer, this form of SP applies directly with no modification. For the attention or SSM operation, aka context parallelism (CP). For attention, one could use Ring attention to split it up along the sequence dimension. For Mamba-2, the SSD framework comes to our help once again: using the same block decomposition, we can have each GPU computing its local output and its final states, then pass the states between GPUs (using send/receive communication primitives), before updating the final output of each GPU.

Variable Length

For finetuning and inference, in the same batch we often have sequences of different lengths. For Transformer, one would usually pad so all sequences have the same length (wasting computation), or implement attention specifically for variable length sequences with careful load-balancing. With SSM, we can simply treat the whole batch as a long “sequence”, and avoid passing the states between different sequences in the batch by setting the state transition $A_t$ to 0 for tokens at the end of each sequence.

Results

How well do these optimizations work? The faster SSD algorithm allows us to increase the state dimension ($\mathtt{N}=64$ or $128$ compared to $\mathtt{N}=16$ in Mamba-1). Even though technically Mamba-2 is more restricted than Mamba-1 for the same $\mathtt{N}$, the larger state dimensions generally improve model quality. Here we show results for models trained on 300B tokens on the Pile, with Mamba-2 outperforming Mamba-1 and Pythia.

What about hybrid models? We have seen from recent and concurrent work (such as Jamba and Zamba) that combining Mamba layers with attention layers can improve over pure Transformer or Mamba. We validate at 2.7B parameters and 300B tokens scale that a hybrid model with just 6 attention blocks (and 58 SSD blocks) outperforms 64 SSD blocks, as well as our standard Transformer++ baseline (32 gated MLP and 32 attention blocks).

We also validated that the SSD algorithm is significantly faster than the selective scan algorithm from Mamba-1 for the same state dimension, and scales much better computationally to larger state dimensions. Getting those tensor cores to go brrr is the key!

Future Directions

With SSD, we have connected (linear) attention and SSMs, allowing us to design faster algorithms and implement systems optimizations for SSMs. There are still tons of exciting directions that we (and hopefully the community) want to tackle:

• Understanding: hybrid models with a few (4-6) attention layers perform very well, even better than pure Mamba(-2) or Transformer++. What are these attention layers doing? Can they be replaced with another mechanism?
• Training optimizations: though SSD might be faster than attention, Mamba-2 as a whole might still be slower than Transformers at short (e.g. 2K) sequence length, since the MLP layers in Transformers are very hardware-friendly. Our implementation of SSD does not specifically take advantage of new features on H100 GPUs, and we look forward to future optimizations that could make SSMs faster to train than Transformers for large-scale pretraining at 2-4K sequence length.
• Inference optimizations: there’s a whole suite of optimizations tailored to Transformers, in particular handling the KV cache (quantization, speculative decoding). How would the inference landscape change if model states (e.g. SSM states) no longer scale with context length, and KV cache is no longer the bottleneck?