State Space Duality (Mamba-2) Part II - The Theory

In Part I of this series, we defined the state space dual (SSD) model. In isolation, this model is relatively simple to define, and we claimed that it can be computed either as an SSM recurrence or with an attention-like pattern. If you just want to use the model, feel free to skip this post!

In this post, we’ll dive into the theory behind the model. We’ll derive the SSD “duality” in two completely separate ways, one starting from the SSM perspective and one from the attention perspective. Each method is actually much more broad than the SSD model itself, and the union of these two strong generalizations is what we call the SSD framework. This framework provides a rich body of connections between state space models, attention, and structured matrices. While the SSD model can be viewed as a specific instantiation of each prong of the framework, the SSD framework is much more general opens up many directions for future work.

The State Space Duality framework

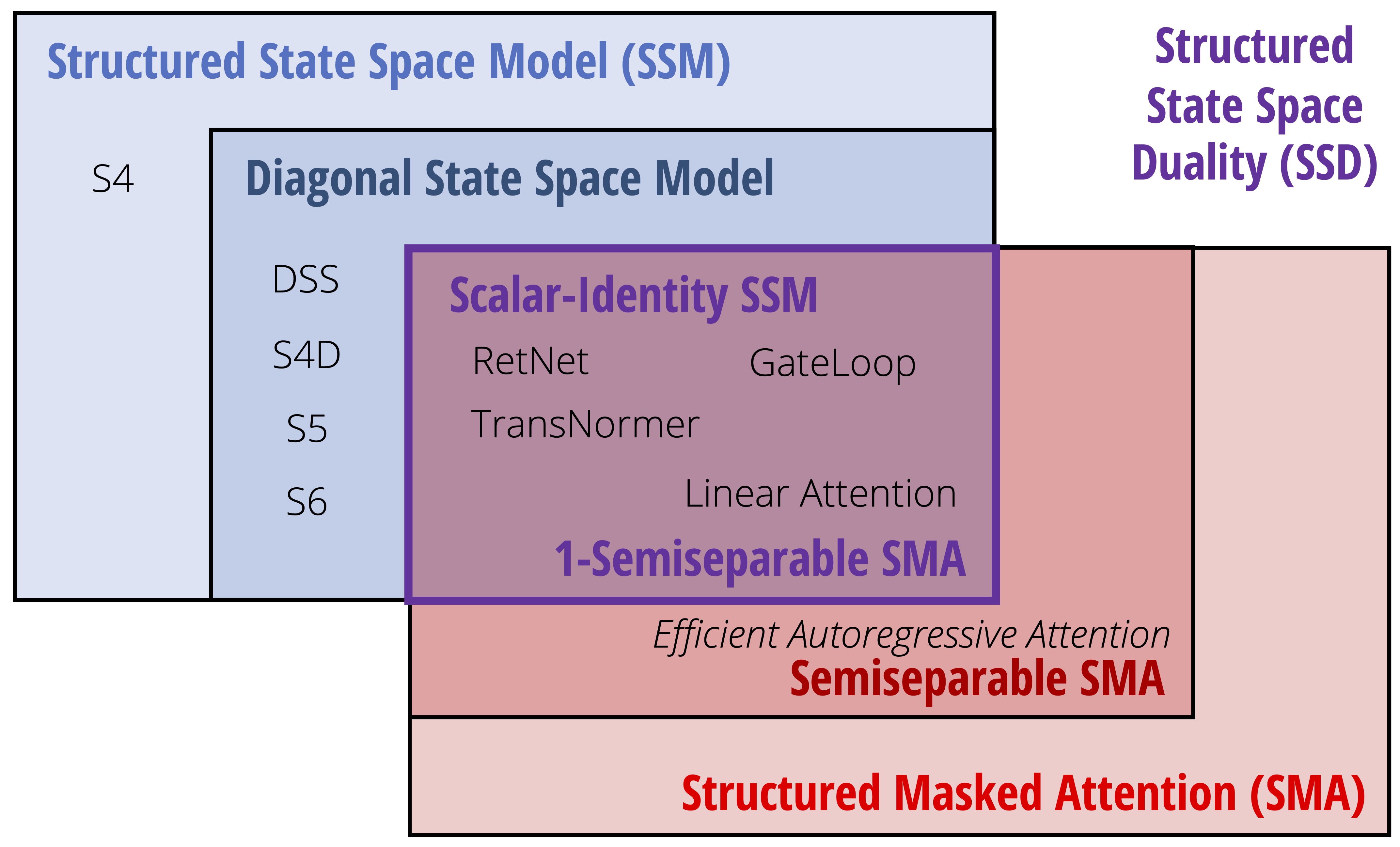
Structured State Space Duality — SSD Framework (red, blue): State space models (i.e. semiseparable matrices) and structured masked attention encapsulate large classes of efficient sequence models. Their intersection is the SSD model (purple).

For each of the two parts of this framework, we’ll

Define the general concepts
Show how the SSD model is an instantiation, and prove the duality
Suggest future directions for how the framework can be used

Note that this theory is not necessary to use the SSD model itself; this part of the series can be safely skipped for the practitioner that just wants to use SSD (Mamba-2).

Recap: The SSD Model

Part I of this series introduced the SSD layer, which is defined as a selective SSM

\[\begin{aligned} h_{t} &= A_t h_{t-1} + B_t x_t \\ y_t &= C_t^{\top} y_t \end{aligned}\]

\begin{equation} \label{eq:ssm} (\text{Selective state space model (SSM)}) \end{equation}

with scalar-identity structure on $A$.

More formally, we view it as a sequence transformation $X \mapsto Y$

\begin{equation} \label{eq:ssm-transformation} Y^\mathtt{(T,P)} = \mathsf{SSM}(A^\mathtt{(T)}, B^\mathtt{(T,N)}, C^\mathtt{(T,N)})(X^\mathtt{(T,P)}) \end{equation}

The dual attention-like form of the SSD layer is

\begin{equation} \label{eq:ssd-attention} M = L \circ C B^\top \in \mathbb{R}^{\mathtt{(T,T)}} \end{equation}

Now let’s see how to prove this!

SSD Framework 1: Structured Matrix Transformations

The first framing of the duality will be from an SSM-centric perspective, where we’ll prove the duality through the framework of matrix sequence transformations or “matrix mixers”.

Matrix Transformations

The idea is that many sequence models, i.e. sequence transformations $X \in \mathbb{R}^\mathtt{(T,P)} \mapsto Y \in \mathbb{R}^\mathtt{(T,P)}$, can be written in the form of a single matrix multiplication $Y = M(X) \cdot X$ where $M$ is a matrix which can itself depend on $X$. We call this a matrix sequence transformation, or matrix transformation for short. In the literature sequence transformations have also been referred to as “sequence mixers” or “token mixers”, and matrix sequence transformations as “matrix mixers”. There are many examples of these, which are distinguished by the structure of the $M$ matrix. The de facto example is self-attention itself, where $M = \mathsf{softmax}(QK^\top)$ is the attention matrix. Other examples include MLP-Mixer, FNet, and Monarch Mixer.

Why do we care about these types of models?

Writing a sequence model as a matrix transformation provides a powerful tool to understand the structure and characteristics of the model.

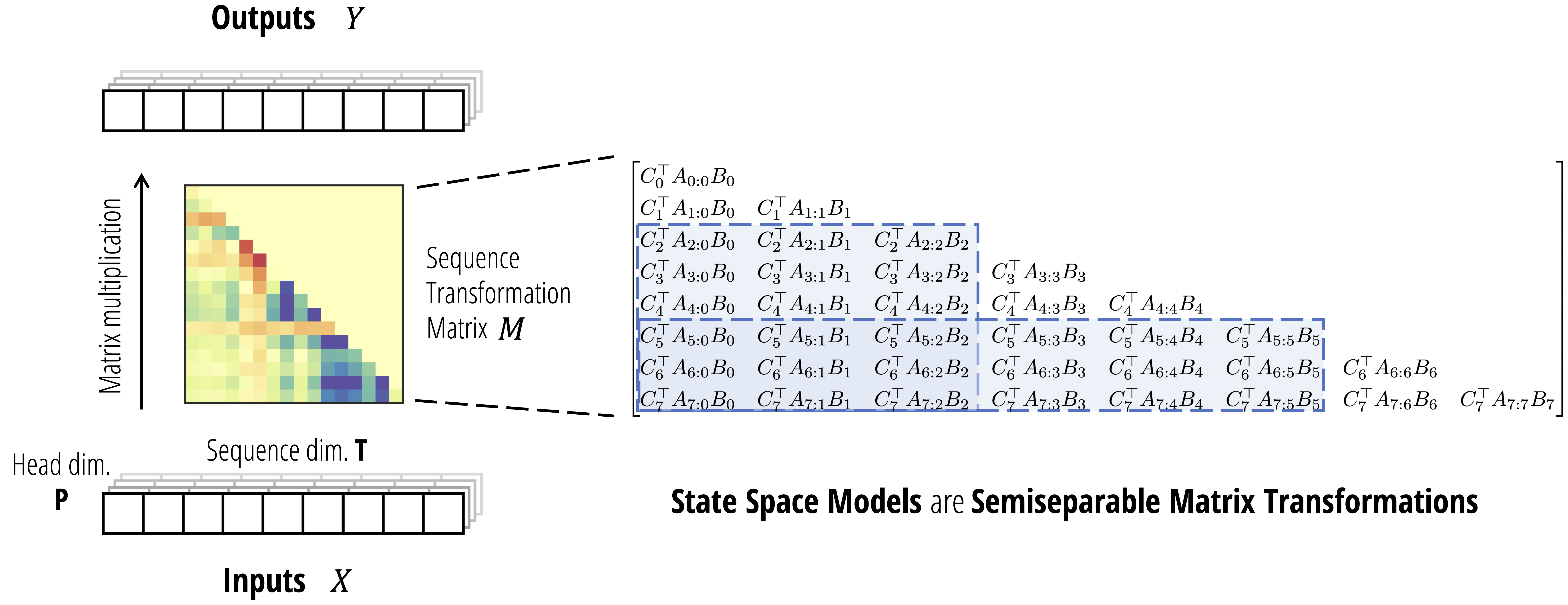
And although general non-linear RNNs such as LSTMs cannot be written as matrix mixers, state space models can! In fact, this is pretty easy to see by just unrolling the definition of the SSM recurrence. The upshot is that the SSM \eqref{eq:ssm-transformation} can be written as a matrix transformation

\[Y = \mathsf{SSM}(A, B, C)(X) = MX\]

where $M_{ij} = 0$ for $i < j$ (i.e. it’s lower triangular) and otherwise \begin{equation} \label{eq:semiseparable} M_{ij} = C_i^\top A_{i:j}^\times B_j := C_i^\top A_i \dots A_{j+1} B_j \end{equation}

Drawing it out, this matrix looks like

\[\begin{bmatrix} C_0^\top B_0 & \\ C_1^\top A_1 B_0 & C_1^\top B_1 & \\ C_2^\top A_2A_1 B_0 & C_2^\top A_2 B_1 & C_2^\top B_2 \\ \vdots & \vdots & \ddots & \ddots \\ C_\mathtt{T}^\top A_{\mathtt{T}-1}\dots A_1 B_0 & C_\mathtt{T}^\top A_{\mathtt{T}-1}\dots A_2 B_1 & \dots & C_\mathtt{T}^\top A_{\mathtt{T}-1} B_{\mathtt{T}-2} & C_\mathtt{T}^\top B_{\mathtt{T}-1} \\ \end{bmatrix}\]

\begin{equation} \label{eq:ssm-matrix} (\text{Matrix Transformation Representation of State Space Models}) \end{equation}

Semiseparable Matrices

This type of matrix in fact has a name: it’s called a (triangular) semiseparable matrix, and has been studied in other fields of engineering and computational linear algebra. These matrices are (IMO) quite fundamental and beautiful, and the full paper talks about more of their properties. For example, an alternative characterization of semiseparable matrices is their structured rank property, which says that every submatrix contained in the lower-triangular portion is low rank.

For our purposes, we’ll care about this form mainly for the algorithmic considerations. One of the central messages of this SSD paper is that:

Takeaway: Computing SSMs Through Matrix Multiplication

All algorithms for computing state space models can be viewed as structured matrix multiplication algorithms on semiseparable matrices.

Let’s see an easy instantiation of this, focusing on our main objective!

Deriving the Duality: SSM to Attention

To show that equation \eqref{eq:ssd-attention} follows from equation \eqref{eq:ssm} (in the case of the SSD model, i.e. scalar SSM), we directly use the matrix form of the state space model \eqref{eq:semiseparable}. Because the $A_t$ are all scalars in this case, they can be factored out of the entries

\[C_i^\top A_{i:j}^\times B_j = A_{i:j}^\times \cdot (C_i^\top B_j)\]

which directly implies equation \eqref{eq:ssd-attention}.

In summary:

Duality Representation 1 (SSM)

The duality for the SSD model can be seen as two different matrix multiplication algorithms on the semiseparable matrix.

The linear form is a structured matrix multiplication algorithm that computes the outputs $Y_0, Y_1, \dots$ sequentially, leveraging the structure of the semiseparable matrix.
The quadratic form is the naive matrix multiplication algorithm that materializes the full matrix.

Going Beyond the SSD Layer 1

The power of the semiseparable matrix representation applies to all state space models, with various downstream implications.

Algorithms

Algorithmically, the Mamba-2 paper explores several consequences, such as:

The above duality result for the SSD model, i.e. a scalar-identity structured SSM.
New asymptotic efficiency results for state space models (Theorem 3.7), which follow from applying known results from the semiseparable matrix literature .
A more general hybrid algorithm that can be viewed as combining both the linear and quadratic forms to get the best of both worlds. This can be derived as a new matrix multiplication algorithm utilizing block decompositions of the semiseparable matrix. This is the subject of Part III of this blog series!

Understanding

Conceptually, the matrix transformation viewpoint helps provide a unifying view of sequence models. Some example downstream ideas include

New sequence models: Restricting ourselves to matrix transformations reduces the problem of developing new sequence models to that of finding structured matrix classes with target properties. In ongoing work by my students, we study this point of view, and use it to derive the most natural bidirectional extension of Mamba (coming very soon!).
Expressivity: Looking at the matrix transformation representation can help us understand what different models can represent from a linear algebraic perspective. In another ongoing work, we use this as a tool to study which subquadratic models are the most amenable to being distilled from Transformers.
Interpretability: A concurrent work derived the matrix formulation of SSMs and use it to probe the internal representations of Mamba models.

We’re excited to see what algorithmic and conceptual ideas from the structured matrix literature can be applied to further improve state space models!

SSD Framework 2: Structured Attention

The second framing of the duality is from an attention-centric perspective, where we’ll prove the duality through the framework of tensor contractions.

Note that this is entirely independent of the previous [matrix transformation viewpoint].

Warm-up: Kernel Attention

For our purposes, we’ll define attention as a function

\[(Q^\mathtt{(T,N)}, K^\mathtt{(S,N)} , V^\mathtt{(S,P)} ) \mapsto Y^\mathtt{(T,P)}\]

given by the pairwise matrix multiplications

\[Y = (QK^\top) \cdot V\]

On Dimensions

Think of $\mathtt{P} = \mathtt{N}$ as the head dimension; technically speaking, in attention the $V$ head dimension $\mathtt{P}$ can differ from the $QK$ head dimension $\mathtt{N}$. Think of $\mathtt{T}$ as the target sequence dimension and $\mathtt{S}$ as the source sequence dimension. Giving these two axes different names will make the math more clear and also covers more general forms of attention such as cross-attention, where the source and target are separate sequences with different lengths. However, for our purposes we’ll assume the self-attention setting where $\mathtt{S}=\mathtt{T}$.

Why can we assume this form?

The usual form of attention $Y = f(QK^\top) \cdot V$ (e.g. where $f$ is the softmax function) can, for essentially all functions $f$And up to some additional massaging such as row-wise normalization, which is easy to handle, be written as $Y = \psi(Q)\psi(K)^\top \cdot V$ for some appropriate feature map $\psi$ (which may be infinite dimensional). In this case, we can simply redefine $Q \leftarrow \psi(Q)$ and define $\mathtt{N}$ to be the feature dimension of the attention kernel to begin with. Softmax attention, for example, can be represented with a particular infinite-dimensional feature map ($\mathtt{N}=\infty$) which represents the exponential kernel.

We’ll restrict ourselves to the case when $\psi$ is finite, which is sometimes called kernel attention. Many, many variants have been proposed before!

Why do we care about this formulation? When the sequence length $\mathtt{T}$ grows and the feature dimension $\mathtt{N}$ is small—commonly, in the regime when $\psi$ is simple such as an elementwise transform and so $\mathtt{N}$ is constant—then the cost of attention can be reduced from quadratic in $\mathtt{T}$ to linear. This follows from simply computing the matrix multiplications in a different order

\[Y = Q \cdot (K^\top V)\]

This is a somewhat “folklore” interpretation of linear attention.At least, one lineage of efficient attention; other varieties exist, such as those based on sparsity or hashing. We reserve the term "linear attention" to those related to Katharopoulos et al., or more broadly low-rank attention.

The most common way of linearizing attention is usually viewed as a consequence of the associativity of matrix multiplication

(Causal) Linear Attention

However, once the basic kernel attention is slightly modified, we can no longer use the associativity of matrix multiplication directly.

The seminal Linear Attention (LA) framework of Katharopoulos et al. shows that it can still be extended to the important case of incorporating causality into attention, for autoregressive settings such as language modeling.

Let’s be a lot more explicit about how it works. The quadratic form of causal linear attention is \begin{equation} \label{eq:quadratic-kernel-attention} Y = (L \circ QK^\top) \cdot V \end{equation} where

\[L = \begin{bmatrix} 1 \\ \vdots & \ddots \\ 1 & \dots & 1 \end{bmatrix}\]

is the causal mask matrix.

The issue is: once the $L$ mask is incorporated into \eqref{eq:quadratic-kernel-attention}, we can no longer directly apply matrix associativity! This is the problem that the original Linear Attention paper addresses. What they show is that \eqref{eq:quadratic-kernel-attention} is equivalent to a different form which avoids materializing the quadratic $QK^\top$ attention matrix and has linear time complexity

\[Y = Q \cdot \mathsf{cumsum}(K^\top V)\]

As far as we’re aware this wasn’t explicitly proved in the paper, although it isn’t too hard to write out the summation to show it.

What we’ll do is prove this equivalence in essentially one line, while revealing exactly where the “linear” part of Linear Attention comes from, and how to strongly generalize it.

Spoiler alert:

Where does the cumsum in Linear Attention come from?

The appearance of the cumulative sum in linear attention is exactly equivalent to the fact that the causal mask $L$, as a matrix multiplication, encodes cumulative sums:
\[y = L \cdot x \iff y = \mathsf{cumsum}(x)\]

A Tensor Contraction Proof of Linear Attention

Let’s write out the quadratic form of linear attention \eqref{eq:quadratic-kernel-attention} very explicitly in tensor contraction or einsum notation, with shape annotations:

\[\begin{aligned} G &= \mathsf{contract}(\mathtt{TN, SN} \to \mathtt{TS})(Q, K) \\ M &= \mathsf{contract}(\mathtt{TS, TS} \to \mathtt{TS})(G, L) \\ Y &= \mathsf{contract}(\mathtt{TS, SP} \to \mathtt{TP})(M, V) \end{aligned}\]

\begin{equation} \label{eq:sma-quad} (\text{Structured Masked Attention - Quadratic Form}) \end{equation}

With this notation, we can notice that this sequence of contractions can be written as a single four-way contraction

\begin{equation} \label{eq:sma} y = \mathsf{contract}(\mathtt{TN},\mathtt{SN},\mathtt{SP},\mathtt{TS} \to \mathtt{TP})(Q, K, V, L) . \end{equation}

And finally, it can be computed with any other contraction ordering. In particular, we can perform pairwise reductions on the order $V, K, L, Q$ instead of $Q, K, L, V$

\[\begin{aligned} Z &= \mathsf{contract}(\mathtt{SP},\mathtt{SN} \to \mathtt{SPN})(V, K) \\ H &= \mathsf{contract}(\mathtt{TS},\mathtt{SPN} \to \mathtt{TPN})(L, Z) \\ Y &= \mathsf{contract}(\mathtt{TN},\mathtt{TPN} \to \mathtt{TP})(Q, H) \end{aligned}\]

\begin{equation} \label{eq:sma-lin} (\text{Structured Masked Attention - Linear Form}) \end{equation}

Now the key observation is that the second line of \eqref{eq:sma-lin} is simply a matrix multiplication by $L$, which can be computed with a cumulative sum.

That’s the entire proof of linear attention! The beauty of it is that we didn’t have to write out a single summation, which was abstracted out into a tensor contraction combined with the structure of $L$.

This immediately proves our claim about the cumsum in linear attention. Moreover, this immediately reveals that the efficiency of linear attention can be made much more general…

Structured Masked Attention

The critical observation is that in order for \eqref{eq:sma-lin} to be fast, all that is necessary is for $L$ to be any structured matrix – in other words any matrix that has subquadratic matrix-vector multiplication.

This immediately motivates one of the main prongs of the SSD framework, which can be seen as a strong generation of LA.

Definition: Structured Masked Attention

Structured masked attention (SMA) is defined as the four-way tensor contraction \eqref{eq:sma} using an attention mask $L$ that is a structured matrix.

Duality Representation 2 (SMA)

SMA has dual quadratic and linearAssuming that the structured matrix $L$ has linear time matrix-vector multiplication modes which are simply two different pairwise reduction orders \eqref{eq:sma-quad} and \eqref{eq:sma-lin}.

Finally, let’s just connect this back to the commonly held view of linear attention as matrix multiplication associativity.

Although it is commonly believed that incorporating attention masks $L$ prevents matrix multiplication reordering, it turns out to still be compatible. In particular, associativity of matrix multiplication is a special case of tensor contraction reduction orders; although the former no longer applies, the latter can integrate the attention mask $L$.

Next, let’s look at some consequences of the structured attention framework.

Deriving the Duality: Attention to SSM

Recall that the SSD model is defined as either a scalar-identity SSM in equation \eqref{eq:ssm}, or through the attention-like form in equation \eqref{eq:ssd-attention}.

To show the equivalence of these forms, we simply recognize that \eqref{eq:ssd-attention} is a special case of structured masked attention where the mask matrix is

\[L = \begin{bmatrix} 1 & \\ a_1 & 1 & \\ a_2a_1 & a_2 & 1 \\ \vdots & \vdots & \ddots & \ddots \\ a_{\mathtt{T}-1}\dots a_1 & a_{\mathtt{T}-1}\dots a_2 & \dots & a_{\mathtt{T}-1} & 1 \\ \end{bmatrix} .\]

\begin{equation} \label{eq:1-ss} (\text{1-semiseparable (1-SS) matrix}) \end{equation}

We call this a 1-semiseparable (1-SS) matrix, for reasons that are explained in more detail in the Mamba-2 paper.

Thus, we can also say that the SSD model is 1-semiseparable masked attention or 1-SS SMA.

To prove that this can be written as an SSM, we simply appeal to the SMA framework, which says that the dual form of this model can be computed through matrix multiplication by $L$. So how fast is that? It’s not too hard to see that multiplication $y = Lx$ can be computed in linear time through a scalar recurrence:

\[\begin{aligned} y_0 &= x_0 \\ y_1 &= a_1 x_0 + a_1 \\ y_2 &= a_2a_1 x_0 + a_2 x_1 + x_2 = a_2 y_1 + x_2 \\ \vdots & \qquad \vdots \end{aligned}\]

This corresponds exactly to the original SSM recurrence!

(In fact, multiplication by 1-SS matrices $L$ can be computed in a lot more ways, which we compile in the full paper! Alternative algorithms can reveal more insights: for example, the associative scan algorithm used by S5 and Mamba can also be shown to be a structured matrix multiplication algorithm on 1-SS matrices.)

Going Beyond the SSD Layer 2

Structured masked attention not only helps define the SSD model and prove its duality, but it is a much broader framework of efficient attention models.

Prior examples include the original linear attention as well as the recent Retentive Network (RetNet) model. These can be viewed as direct special cases of SSD. But beyond SSD, we can define classes of efficient attention by replacing the mask $L$ with any structured matrix. As a suggestion, we think that Toeplitz or Fourier structured attention may be interesting to consider because they might encode different forms of positional information.

Additionally, other forms of structure can be incorporated into the $L$ mask. For example, another extension my students are developing is viewing SSD (and recurrences in general) as an algorithm operating on directed line graphs, and generalizing it to incorporate arbitrary graph structures.

State Space Duality

We’ll end this post with a brief recap of what we’ve covered.

The SSD framework consists of the two broad approaches covered in this post, which is summarized by the two areas of the [Venn diagram]:

Viewing state space models through [structured matrix transformations]
Generalizing linear attention through [tensor contractions]

The [SSD layer] is a particular model which is the purple intersection in the figure, which can be viewed as an instance of either part of the SSD framework, and in particular has dual quadratic and linear forms that can be derived from either representation.

SSD Framework	Structured SSMs	Structured Attention
The main representation is…	Structured matrix \eqref{eq:ssm-matrix} sequence transformations	The 4-way \eqref{eq:sma} tensor contraction
This generalizes…	State space models	Linear attention
The SSD model is an instantiation as…	Scalar state space model ($A_t$ is a scalar-identity matrix)	1-semiseparable masked attention ($L$ mask is a 1-SS matrix)
The linear-quadratic duality is revealed through…	Structured matrix multiplication algorithms	Tensor contraction reduction orderings

Next Up

In the next part of this series, we’ll see how to use some of the SSD framework (in particular, the structured matrix algorithm point of view) to derive the more efficient hybrid SSD algorithm that leverages both of the dual forms.